The Porus Mirror Problem, Part 1

The porus mirror problem

I’m pretty sure I came up with this problem on my own, but I’m not sure if its an existing problem under a different name. Anyway, the situation is as such:

1. We have a very short cylindrical tube. In fact, we’ll ignore the third dimension and just use a circle. For simplicity, we’re using units such that the radius is 1.
2. The tube is filled with a gas that emits corpuscles in one large burst. We assume a large enough number that we can model them continuously. We additionally assume that the emmissions are uniform in location and direction.
3. The tube itself is semitransparent, with transparency determined by a function \(t: [0, 2\pi] \to [0, 1]\) of angle around the circle. Any light that does not pass through is reflected across the normal.

We wish to calculate at each point along the surface of the tube what is the total quantity of light emitted in each direction, from which we can easily calculate the light pattern this system will cast on any shape outside.

The general idea behind the solution

Each beam of light will bounce around withn the tube some number of times. If we formally consider that a zero-energy corpuscle is reflected by a transparent part of the tube, then we have an infinite number of bounces. Since we do not care about time, we can ignore its effects and parameterize our equations discretely in terms of bounces.

In short, we define a family of functions \(L_n (\phi, \theta)\) that describe the intensity of the light at the \(n\)th bounce on the surface of the circle at location \(\theta\) with direction \(\phi\). The result is merely the sum of these functions over all natural numbers.

Finding \(L_0\)

\(L_0(\phi, \theta)\) is our base case, the amount of light in any direction that initially hits at a given point. Finding this value directly appears to be a fairly complex geometric problem involving finding the length of the chord (since only origins along this line could produce light that would be in the correct direction).

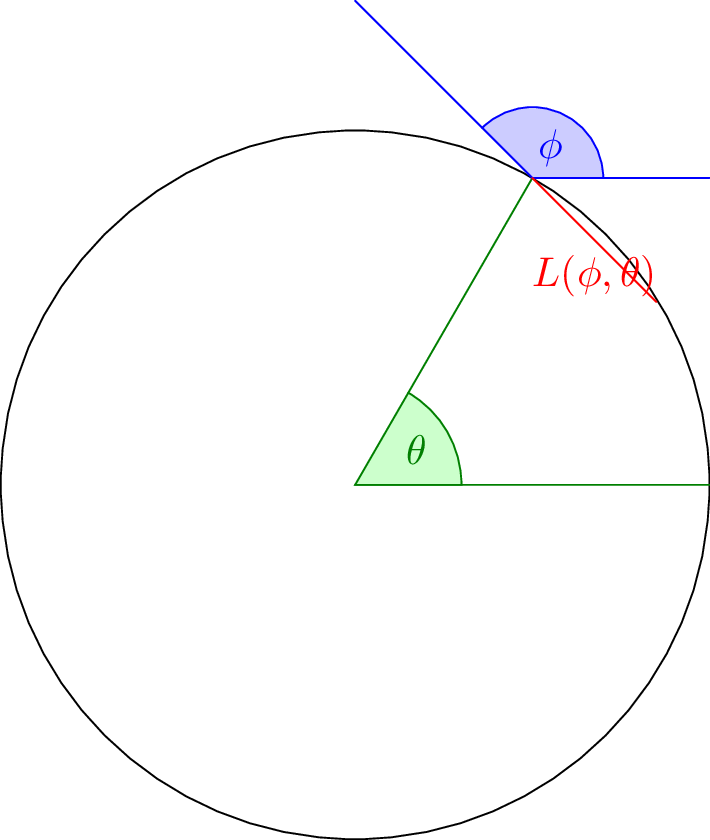
However, if we rotate into the \(\phi\) frame, we end up with the much simpler situation:

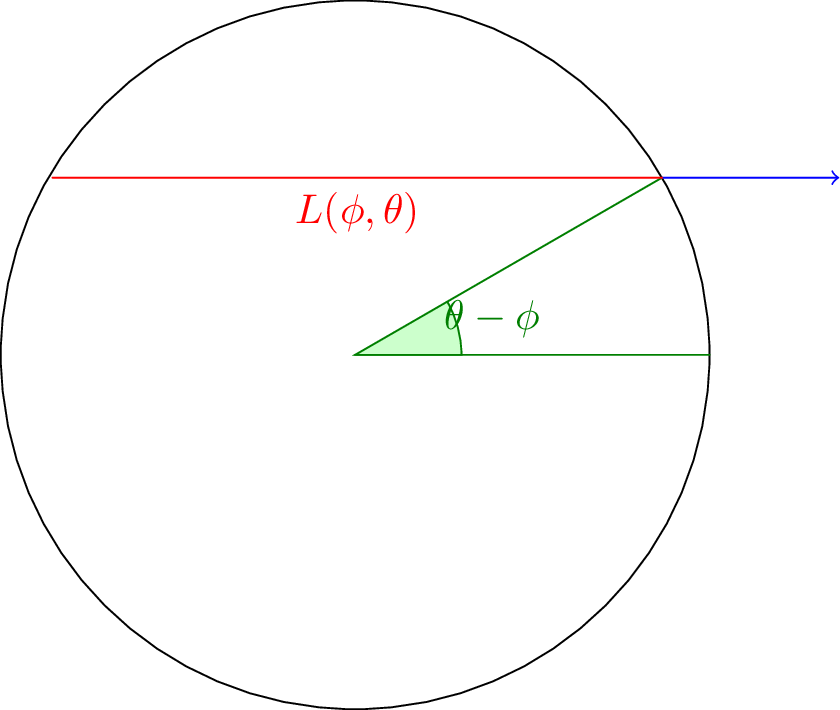
We can fairly simply see that the chord length is \(2 \cos \theta\) to the right of the \(x\)-axis and \(0\) to the left. To avoid an ugly peicewise definition, we can note that this is basically the result of zeroing out cosine when its negative and doublign it when it is positive, yielding the equation \(L_0 = |\cos\theta| + \cos\theta\). Rotating back, we have

\[L_0 = | \cos (\theta - \phi) | + \cos (\theta - \phi) \]

Finding \(L_n\) for higher \(n\)

We can set up a similar situation as for \(L_0\) to find \(L_n\). Basically, it is entirely a result of the reflection from \(L_{n-1}\). The geometry is again fairly complicated, looking like this:

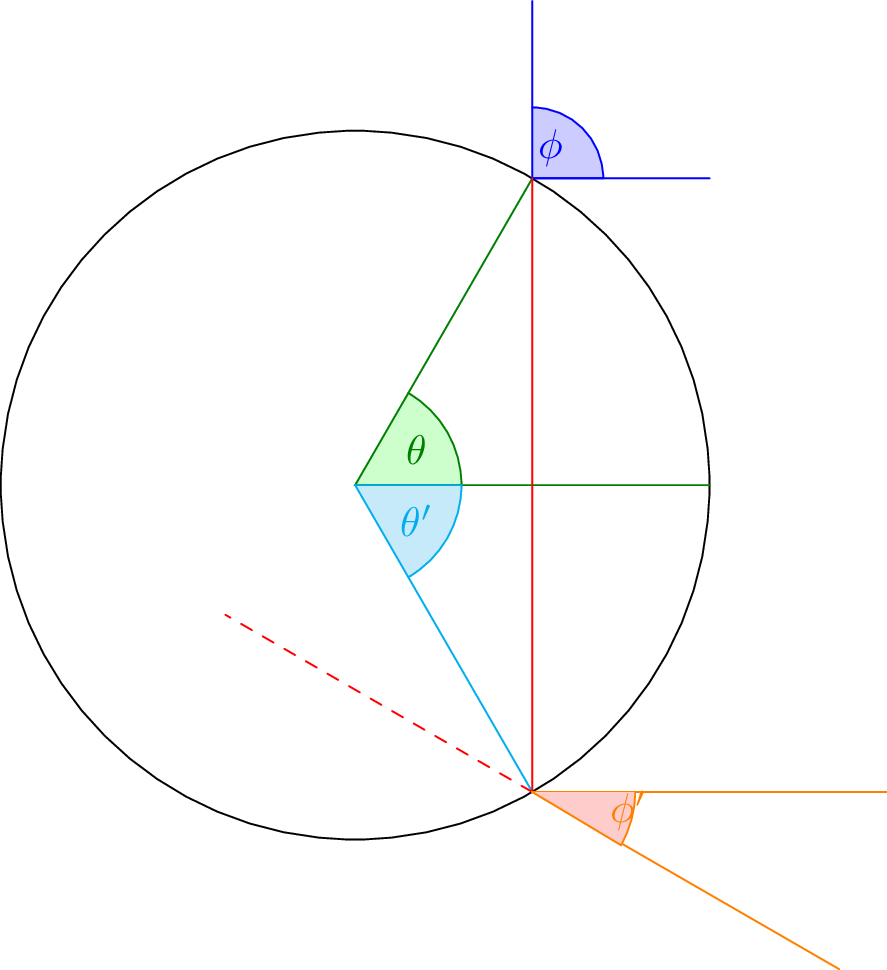
However, the equation ends up being quite simple. We know that the amount of light reflected from the previous bounce is

\[L_n (\theta,\phi) = L_{n-1}(\theta’,\phi’) t(theta’) \]

Rotating in a similar manner, we get:

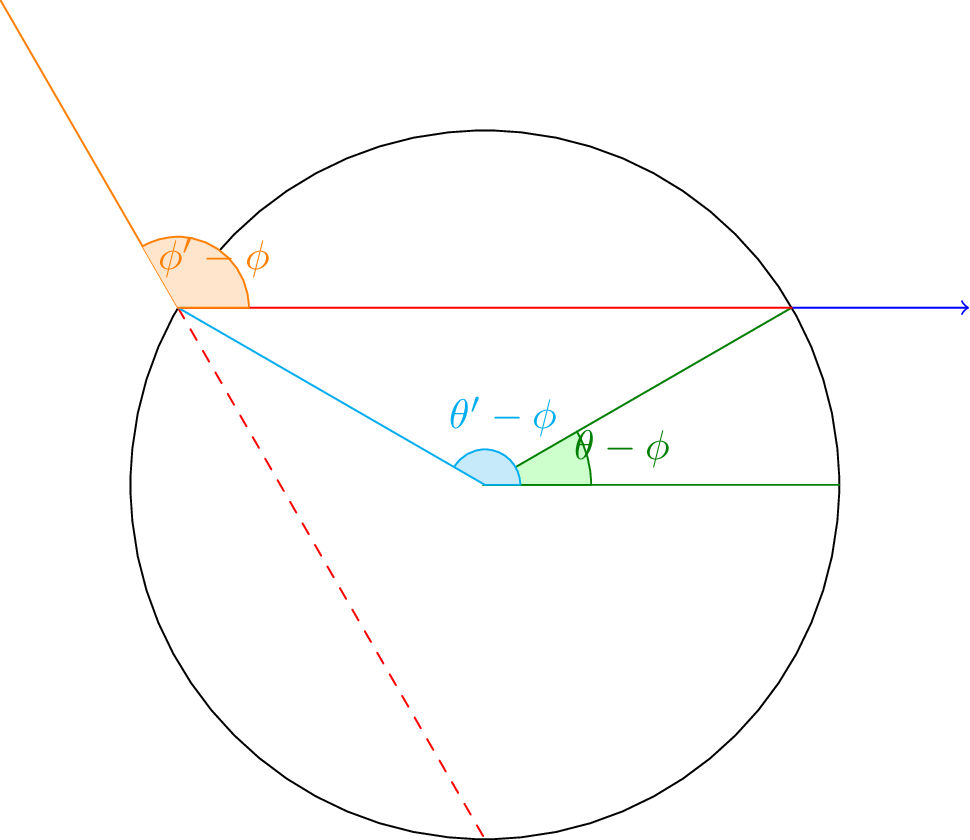
Using this diagram, we can see that the following relation holds.

\[(\theta - \phi) + \frac{\pi - \phi’ + \phi}{2} + (\theta’ - \phi) = \pi\]

We can therefore get the equation: \(2\theta’ -\phi’ = \pi + 3\phi - 2\theta\).

To find \(\phi’\) we can rotate, this time into the \(\theta’\) frame.

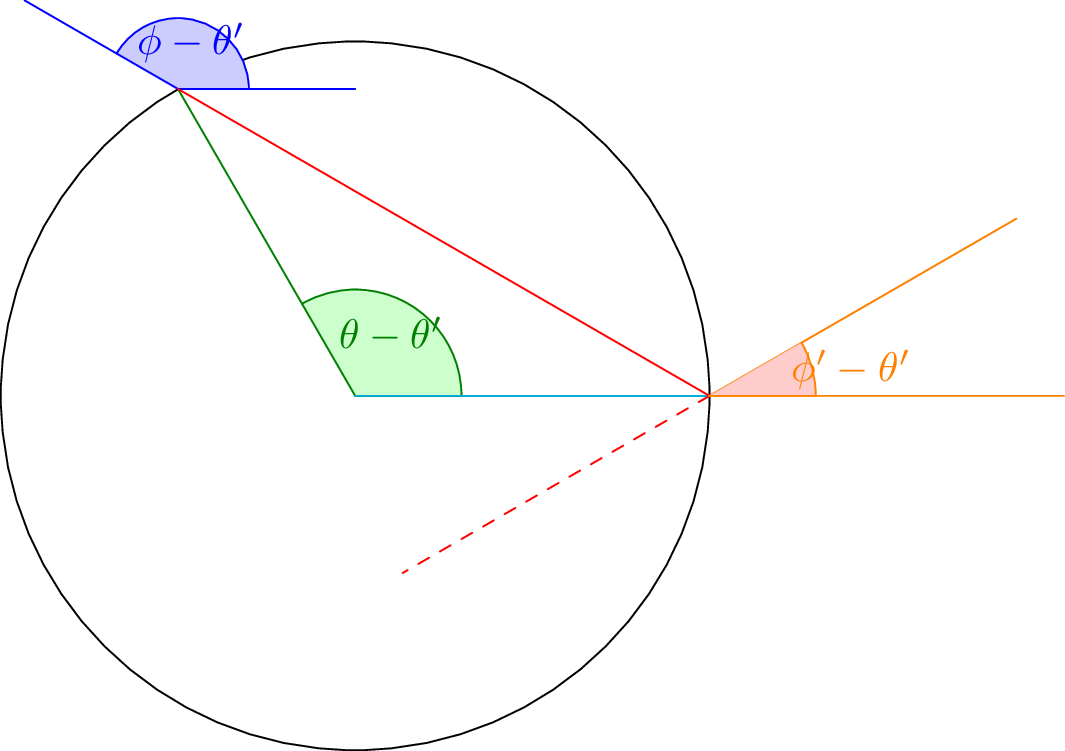
From this, we can find that the three angles of the central triangle are:

\[\frac{\pi - (\phi - \theta’)}{2}, \theta-\theta’, \phi’-\theta’\] \[\pi - (\phi - \theta’) + 2\theta - 2\theta’ + 2\phi’ - 2\theta’ = 2\pi\] \[2\phi’ - 3\theta’= \pi + \phi - 2\theta\]

We can solve the linear system created by this equation and the above:

\[\theta’ = \pi - 6\theta + 7\phi\] \[\phi’ = \pi - 10\theta + 11\phi\]

Therefore, we have the relation:

\[L_n(\theta, \phi) = L_{n-1}(\pi - 6\theta + 7\phi, \pi - 10\theta + 11\phi) (1 - t(\pi - 6\theta + 7\phi))\]

To be continued

OK, so we now have a base case and a recursive case for \(L\) as a function of time. Next time, I’ll actually do some calculations and demonstrate how it looks on some porus mirrors.

Correction

An earlier version of this article had inaccurate equations, they have been fixed.