Sampling: A Different Kind of Election "Map"

20 Jun 2022

Election maps tend to obscure a couple things that I think are interesting about American elections.

First, about 33% of Trump supporters, and about 30% of Biden supporters lived in precincts that voted for the other party, so show up in the other party’s color on the map!

Second, the map tends to overstate the number of people who live in purely rural areas.

The combination of these two effects leads to in my view a fairly big distortion of our pictures of blue and red America, but especially red America, which people begin to picture as entirely middle-of-nowhere rural areas.

Instead, here’s a sampling of 1000 voters and what their neighborhoods look like. This has the benefit of giving you a picture of what Biden’s America and Trump’s America look like: not two disjoint nations, but two overlapping and intertwined distributions. You can click each dot to jump down to the voter represented by the dot.

Biden’s voters are placed on the left, while Trump’s are on the right. I have provided an image of what their street might look like on Google Streetview, as well as the lean of their precinct. If you click on the image, it will take you to a Google maps link for their precinct’s center, so you can see where it is.

I think, beyond everything else, one of the biggest takeaways I have is just how empty suburban areas in the South and Midwest are. I grew up in a fairly dense suburb of LA, where lot sizes are about a sixth of an acre and have lived in small cities ever since, so I pictured, e.g., “Georgia suburbs” to be similar. Instead, they look a lot like what I picture when someone says “rural America”.

Technical details: to sample the voters I first figured out how many Trump and how many Biden voters should be picked, then for each candidate I sampled precincts randomly, weighted by how many of that candidate’s voters lived in the precinct. I excluded Kentucky from this sampling as I do not have precinct data for Kentucky. The precinct data is from a combination of the NYT and VEST and I try to find a street with a “street-like” address (so not a freeway or major road) inside the precinct, whenever possible. The images should be taken as a broadstrokes vibe of the precinct rather than something super specific.

Voter 1's Neighborhood 27°37'0"N 80°28'21"W approx. 7017, 8th Street, Indian River County, Florida, 32968, United States Precinct Margin: R+24%	Voter 2's Neighborhood 34°6'50"N 84°34'53"W approx. JD's Bar-B-Que, 6426, Bells Ferry Road, Southfork, Woodstock, Cherokee County, Georgia, 30189, United States Precinct Margin: R+36%
Voter 3's Neighborhood 37°41'40"N 122°7'3"W approx. Edendale Middle School, 16160, Ashland Avenue, San Lorenzo, Alameda County, California, 94580, United States Precinct Margin: D+60%	Voter 4's Neighborhood 35°51'29"N 80°4'38"W approx. 113, Maplewood Avenue, Fair Grove, Thomasville, Davidson County, North Carolina, 27360, United States Precinct Margin: R+65%
Voter 5's Neighborhood 40°37'12"N 74°47'59"W approx. Cushetunk Mountain Nature Preserve, Yellow Trail, Readington Township, Hunterdon County, New Jersey, 08833, United States Precinct Margin: R+12%	Voter 6's Neighborhood 35°27'50"N 81°1'18"W approx. New Hope Baptist Church, North Little Egypt Road, Lincoln County, North Carolina, 28037, United States Precinct Margin: R+42%
Voter 7's Neighborhood 38°44'36"N 121°20'29"W approx. Vineyard Road, Placer County, California, 95678, United States Precinct Margin: R+6%	Voter 8's Neighborhood 33°29'12"N 81°33'47"W approx. 1967, Joyner Pond Road, Aiken County, South Carolina, 29803, United States Precinct Margin: R+38%
Voter 9's Neighborhood 42°58'0"N 78°50'59"W approx. 295, Hartford Avenue, Ellwood Park, Buffalo, Erie County, New York, 14223, United States Precinct Margin: D+32%	Voter 10's Neighborhood 45°12'23"N 93°19'10"W approx. 2090, 130th Avenue Northwest, Oaks, Coon Rapids, Anoka County, Minnesota, 55448, United States Precinct Margin: D+4%
Voter 11's Neighborhood 31°51'53"N 81°42'24"W approx. 1472, Hodges Road, Liberty County, Georgia, 31313, United States Precinct Margin: R+1%	Voter 12's Neighborhood 48°8'17"N 122°17'10"W approx. 3944, Rose Road, Lake Goodwin, Snohomish County, Washington, 98292, United States Precinct Margin: R+5%
Voter 13's Neighborhood 41°41'7"N 71°27'29"W approx. 124, Cowesett Road, Cowesett, Warwick, Kent County, Rhode Island, 02886, United States Precinct Margin: D+13%	Voter 14's Neighborhood 44°18'43"N 105°28'29"W approx. 420, Meadow Rose Avenue, Gillette, Campbell County, Wyoming, 82716, United States Precinct Margin: R+83%
Voter 15's Neighborhood 34°5'44"N 118°12'28"W approx. PetrolX, N Figueroa Street, Highland Park, Los Angeles, Los Angeles County, California, 90065, United States Precinct Margin: D+72%	Voter 16's Neighborhood 29°31'41"N 98°39'9"W approx. 8422, Brixton Street, Braun Station, San Antonio, Bexar County, Texas, 78254, United States Precinct Margin: D+0%
Voter 17's Neighborhood 35°56'50"N 78°55'36"W approx. 112, Grey Elm Trail, Durham, Durham County, North Carolina, 27713, United States Precinct Margin: D+70%	Voter 18's Neighborhood 29°35'8"N 82°0'24"W approx. 110, Floradandy Road, Putnam County, Florida, 32640, United States Precinct Margin: R+33%
Voter 19's Neighborhood 37°7'57"N 76°23'27"W approx. 562, Wythe Creek Road, Rivergate, Poquoson, Virginia, 23662, United States Precinct Margin: R+43%	Voter 20's Neighborhood 36°18'23"N 119°23'1"W approx. Aviation Way, Visalia, Tulare County, California, United States Precinct Margin: R+16%
Voter 21's Neighborhood 29°37'47"N 95°34'49"W approx. Cash Road, Stafford, Fort Bend County, Texas, 77477, United States Precinct Margin: D+19%	Voter 22's Neighborhood 40°55'3"N 73°51'50"W approx. Yonkers Raceway, Trenchard Street, Dunwoodie Heights, City of Yonkers, Westchester County, New York, 10704, United States Precinct Margin: R+19%
Voter 23's Neighborhood 40°27'18"N 80°3'58"W approx. 3411, Chartiers Avenue, Sheraden, Pittsburgh, Allegheny County, Pennsylvania, 15204, United States Precinct Margin: D+37%	Voter 24's Neighborhood 40°37'0"N 73°58'52"W approx. 2113, 62nd Street, Brooklyn, Kings County, City of New York, New York, 11204, United States Precinct Margin: D+8%
Voter 25's Neighborhood 40°4'24"N 80°40'21"W approx. 31, Jenna Way, Royal Oak Estates, Wheeling, Ohio County, West Virginia, 26003, United States Precinct Margin: R+21%	Voter 26's Neighborhood 35°57'36"N 77°53'59"W approx. 1199, South Old Carriage Road, Westry, Rocky Mount, Nash County, North Carolina, 27804, United States Precinct Margin: R+20%
Voter 27's Neighborhood 38°59'26"N 94°16'14"W approx. 2898, Southwest 3rd Street Terrace, Blue Springs, Jackson County, Missouri, 64014, United States Precinct Margin: R+17%	Voter 28's Neighborhood 45°49'12"N 90°26'36"W approx. Voight Road, Town of Fifield, Price County, Wisconsin, 54524, United States Precinct Margin: R+28%
Voter 29's Neighborhood 45°36'15"N 94°11'32"W approx. Maple Avenue, Sauk Rapids, Benton County, Minnesota, 5377, United States Precinct Margin: R+13%	Voter 30's Neighborhood 41°17'16"N 85°47'38"W approx. 99, EMS C28E Lane, Island Park, Kosciusko County, Indiana, 46582, United States Precinct Margin: R+54%
Voter 31's Neighborhood 47°31'14"N 122°36'11"W approx. 3577, Lund Avenue Southeast, Parkwood, Conifer Park, Kitsap County, Washington, 98366, United States Precinct Margin: D+7%	Voter 32's Neighborhood 35°52'3"N 86°28'27"W approx. 4386, Pretoria Run, Butler Estates, Murfreesboro, Rutherford County, Tennessee, 37128, United States Precinct Margin: R+14%
Voter 33's Neighborhood 40°18'7"N 75°21'37"W approx. 515, Meetinghouse Road, Franconia, Franconia Township, Montgomery County, Pennsylvania, 18964, United States Precinct Margin: R+19%	Voter 34's Neighborhood 40°17'23"N 83°57'38"W approx. 247, Jefferson Street, Quincy, Miami Township, Logan County, Ohio, 43343, United States Precinct Margin: R+71%
Voter 35's Neighborhood 40°48'51"N 74°29'47"W approx. 116, Lake Road, Butterworth Farms, Morris Plains, Morris Township, Morris County, New Jersey, 07960, United States Precinct Margin: D+25%	Voter 36's Neighborhood 42°49'14"N 71°14'7"W approx. 96, High Street, Salem, Rockingham County, New Hampshire, 03079, United States Precinct Margin: R+13%
Voter 37's Neighborhood 38°31'27"N 122°44'41"W approx. Pond Trail, Santa Rosa, Sonoma County, California, 95439, United States Precinct Margin: D+42%	Voter 38's Neighborhood 33°52'14"N 118°22'25"W approx. 2112, Carnegie Lane, El Nido, Redondo Beach, Los Angeles County, California, 90278, United States Precinct Margin: D+47%
Voter 39's Neighborhood 39°44'51"N 104°58'16"W approx. 1375, East 20th Avenue, City Park West, Denver, Colorado, 80205, United States Precinct Margin: D+75%	Voter 40's Neighborhood 33°52'56"N 117°52'17"W approx. 451, West Madison Avenue, Old Town Placentia, Placentia, Orange County, California, 92870, United States Precinct Margin: R+1%
Voter 41's Neighborhood 32°23'35"N 111°3'40"W approx. 4513, West Mesquital del Oro, Pima County, Arizona, 85742, United States Precinct Margin: R+9%	Voter 42's Neighborhood 30°26'49"N 97°46'23"W approx. 8405, Foxhound Trail, Hunter's Chase, Jollyville, Austin, Williamson County, Texas, 78729, United States Precinct Margin: D+44%
Voter 43's Neighborhood 28°1'37"N 82°35'9"W approx. 8911, Saddletree Way, Hillsborough County, Florida, 33635, United States Precinct Margin: D+22%	Voter 44's Neighborhood 43°10'15"N 79°2'29"W approx. 505, Cayuga Street, Lewiston Heights, Village of Lewiston, Town of Lewiston, Niagara County, New York, 14092, United States Precinct Margin: D+4%
Voter 45's Neighborhood 36°34'57"N 93°6'52"W approx. 1705, Savage Road, Mincy, Taney County, Missouri, 65679, United States Precinct Margin: R+62%	Voter 46's Neighborhood 34°3'4"N 118°6'46"W approx. 1057, South Orange Avenue, Monterey Park, Los Angeles County, California, 91755, United States Precinct Margin: D+37%
Voter 47's Neighborhood 36°31'36"N 79°40'53"W approx. 11247, East Meadow Road, Green Acres, Draper Village, Rockingham County, North Carolina, 27288, United States Precinct Margin: R+26%	Voter 48's Neighborhood 40°43'53"N 86°13'54"W approx. 7482, East 250 S, Cass County, Indiana, 46994, United States Precinct Margin: R+59%
Voter 49's Neighborhood 33°58'28"N 83°57'18"W approx. 411, Grenier Terrace Northeast, Gwinnett County, Georgia, 30045, United States Precinct Margin: D+53%	Voter 50's Neighborhood 38°55'57"N 95°53'29"W approx. 7421, Southwest Docking Road, Shawnee County, Kansas, 66402, United States Precinct Margin: R+37%
Voter 51's Neighborhood 34°2'23"N 118°13'50"W approx. Santa Fe Avenue, Arts District, Downtown, Los Angeles, Los Angeles County, California, 90021, United States Precinct Margin: D+75%	Voter 52's Neighborhood 30°16'32"N 87°40'5"W approx. 900, East 22nd Avenue, Gulf Shores, Baldwin County, Alabama, 36542, United States Precinct Margin: R+54%
Voter 53's Neighborhood 43°4'39"N 87°53'58"W approx. Roverwest Dog Exercise Area, North Bremen Street, Riverwest, Milwaukee, Milwaukee County, Wisconsin, 53212, United States Precinct Margin: D+77%	Voter 54's Neighborhood 43°43'5"N 84°20'22"W approx. 3675, North Hope Road, Lincoln Township, Midland County, Michigan, 48642, United States Precinct Margin: R+29%
Voter 55's Neighborhood 40°35'57"N 75°23'57"W approx. 603, Sayre Street, Fountain Hill, Lehigh County, Pennsylvania, 18015, United States Precinct Margin: D+30%	Voter 56's Neighborhood 33°46'11"N 92°7'21"W approx. Huddleston Road, Cleveland County, Arkansas, 71660, United States Precinct Margin: R+56%
Voter 57's Neighborhood 41°9'25"N 96°2'24"W approx. Rolling Hills Church, North Monroe Street, Papillion, Sarpy County, Nebraska, 68046, United States Precinct Margin: R+12%	Voter 58's Neighborhood 41°41'33"N 83°36'7"W approx. Telephone Exchange Central Office, 2414, West Sylvania Avenue, Deveaux, Fitch, Toledo, Lucas County, Ohio, 43560, United States Precinct Margin: D+15%
Voter 59's Neighborhood 37°13'41"N 121°59'12"W approx. 18, Ellenwood Avenue, Los Gatos, Santa Clara County, California, 95030, United States Precinct Margin: D+48%	Voter 60's Neighborhood 33°19'45"N 111°48'1"W approx. 12911, South 131st Street, Gilbert, Maricopa County, Arizona, 85233, United States Precinct Margin: R+3%
Voter 61's Neighborhood 45°40'43"N 121°32'32"W approx. 1600, Tucker Road, Hood River County, Oregon, 97031, United States Precinct Margin: D+19%	Voter 62's Neighborhood 30°23'10"N 91°56'6"W approx. 1099, East G Land Road, St. Martin Parish, Louisiana, 70512, United States Precinct Margin: R+66%
Voter 63's Neighborhood 30°23'24"N 89°5'13"W approx. 3225, 20th Avenue, Gulfport, Harrison County, Mississippi, 39501, United States Precinct Margin: D+41%	Voter 64's Neighborhood 36°4'5"N 82°59'18"W approx. 1319, Culbertson Road, Greene County, Tennessee, 37743, United States Precinct Margin: R+70%
Voter 65's Neighborhood 41°49'48"N 71°23'27"W approx. 15, Taber Avenue, Wayland, Providence, Providence County, Rhode Island, 02906, United States Precinct Margin: D+80%	Voter 66's Neighborhood 33°8'58"N 96°55'38"W approx. 7628, Snug Harbor Circle, Denton County, Texas, 75036, United States Precinct Margin: D+9%
Voter 67's Neighborhood 39°45'28"N 84°10'11"W approx. 41, Drummer Avenue, Saint Annes Hill Historic District, Dayton, Montgomery County, Ohio, 45403, United States Precinct Margin: D+42%	Voter 68's Neighborhood 38°2'54"N 87°22'31"W approx. 582, West Taylor Avenue, Chandler, Warrick County, Indiana, 47610, United States Precinct Margin: R+13%
Voter 69's Neighborhood 34°33'27"N 112°20'22"W approx. 7210, East Sienna Springs Lane, Prescott Valley, Yavapai County, Arizona, 86314, United States Precinct Margin: R+39%	Voter 70's Neighborhood 33°40'10"N 117°17'40"W approx. 31643, Chaparral Way, Lake Elsinore, Riverside County, California, 92532, United States Precinct Margin: D+1%
Voter 71's Neighborhood 45°4'15"N 93°22'46"W approx. 6377, Sumter Avenue North, Brooklyn Park, Hennepin County, Minnesota, 55428, United States Precinct Margin: D+42%	Voter 72's Neighborhood 26°25'54"N 81°44'18"W approx. 21008, Torre Del Lago Street, Bella Terra, Lee County, Florida, 33928, United States Precinct Margin: R+31%
Voter 73's Neighborhood 35°54'36"N 78°55'35"W approx. 604, Forge Road, Crooked Creek, Durham, Durham County, North Carolina, 27713, United States Precinct Margin: D+74%	Voter 74's Neighborhood 41°34'27"N 72°23'44"W approx. 232, Cato Corner Road, North Westchester, Colchester, New London County, Connecticut, 06415, United States Precinct Margin: D+8%
Voter 75's Neighborhood 35°46'50"N 78°37'33"W approx. E Edenton St at Idlewild Ave, East Edenton Street, Idlewild, Seaboard Station, Raleigh, Wake County, North Carolina, 27601, United States Precinct Margin: D+88%	Voter 76's Neighborhood 36°48'43"N 76°23'41"W approx. 308, Snead Fairway, Manor View, Portsmouth City, Virginia, 23701, United States Precinct Margin: R+22%
Voter 77's Neighborhood 42°36'15"N 83°6'35"W approx. 5768, John R Road, Troy, Oakland County, Michigan, 48085, United States Precinct Margin: D+7%	Voter 78's Neighborhood 45°17'42"N 92°41'53"W approx. 263rd Street, Town of Farmington, Polk County, Wisconsin, 54020, United States Precinct Margin: R+35%
Voter 79's Neighborhood 38°54'1"N 77°0'55"W approx. 303, H Street Northwest, Mount Vernon Square, Washington, District of Columbia, 20548, United States Precinct Margin: D+88%	Voter 80's Neighborhood 33°36'59"N 117°51'16"W approx. 2101, Yacht Wanderer, Newport Beach, Orange County, California, 92660, United States Precinct Margin: R+8%
Voter 81's Neighborhood 42°18'37"N 88°51'30"W approx. 10810, Caledonia Road, Belvidere Township, Boone County, Illinois, 61008, United States Precinct Margin: R+19%	Voter 82's Neighborhood 31°53'13"N 82°34'4"W approx. 299, Joe Hester Road, Hazlehurst, Jeff Davis County, Georgia, 31539, United States Precinct Margin: R+73%
Voter 83's Neighborhood 41°6'11"N 85°6'22"W approx. 2911, Rolston Street, Fort Wayne, Allen County, Indiana, 46805, United States Precinct Margin: D+5%	Voter 84's Neighborhood 37°45'51"N 120°50'19"W approx. 487, Pedersen Road, Oakdale, Stanislaus County, California, 95361, United States Precinct Margin: R+31%
Voter 85's Neighborhood 32°48'29"N 117°13'35"W approx. 4809, Beryl Way, Pacific Beach, San Diego, San Diego County, California, 92109, United States Precinct Margin: D+41%	Voter 86's Neighborhood 44°2'38"N 121°12'12"W approx. 61762, Teal Road, Deschutes County, Oregon, 97702, United States Precinct Margin: R+20%
Voter 87's Neighborhood 41°25'41"N 87°40'44"W approx. 650, Clover Lane, Park Forest South, University Park, Will County, Illinois, 60484, United States Precinct Margin: D+83%	Voter 88's Neighborhood 27°25'51"N 82°34'21"W approx. 7, U Avenue, Bayshore Windmill Village, Manatee County, Florida, 34207, United States Precinct Margin: R+6%
Voter 89's Neighborhood 37°40'47"N 121°2'41"W approx. 2728, Sparks Way, Modesto, Stanislaus County, California, 95350, United States Precinct Margin: D+24%	Voter 90's Neighborhood 33°36'48"N 86°40'41"W approx. 1096, Springville Road, Spring Lake Estates, Birmingham, Jefferson County, Alabama, 35215, United States Precinct Margin: D+65%
Voter 91's Neighborhood 32°56'20"N 96°38'43"W approx. 1375, Wagon Wheel Road, Garland, Dallas County, Texas, 75040, United States Precinct Margin: R+2%	Voter 92's Neighborhood 38°55'47"N 104°44'58"W approx. 4239, Ginger Cove Place, Newport Heights, Colorado Springs, El Paso County, Colorado, 80923, United States Precinct Margin: R+17%
Voter 93's Neighborhood 42°45'35"N 73°52'26"W approx. White Course, Central Court Trailer Park, Lisha Kill, Town of Colonie, Albany County, New York, 12205-4221, United States Precinct Margin: R+2%	Voter 94's Neighborhood 32°28'14"N 96°0'54"W approx. 1605, County Road 2421, Van Zandt County, Texas, 75103, United States Precinct Margin: R+78%
Voter 95's Neighborhood 42°9'57"N 73°20'47"W approx. 99, Brush Hill Road, Brookside, Great Barrington, Berkshire County, Massachusetts, 01230, United States Precinct Margin: D+67%	Voter 96's Neighborhood 41°2'10"N 73°45'59"W approx. 45, Barker Avenue, City of White Plains, Westchester County, New York, 10601, United States Precinct Margin: D+49%
Voter 97's Neighborhood 35°44'48"N 79°20'4"W approx. 197, Evans Chapel Road, Town of Siler City, Chatham County, North Carolina, 27344, United States Precinct Margin: R+14%	Voter 98's Neighborhood 38°52'41"N 121°16'24"W approx. 500, Snapdragon Lane, Lincoln, Placer County, California, 95648, United States Precinct Margin: D+0%
Voter 99's Neighborhood 43°46'33"N 87°57'28"W approx. Woodland Road, Town of Plymouth, Sheboygan County, Wisconsin, 53085, United States Precinct Margin: R+31%	Voter 100's Neighborhood 41°31'25"N 73°4'13"W approx. 119, Taft Pointe, Waterbury, New Haven County, Connecticut, 06708, United States Precinct Margin: D+0%
Voter 101's Neighborhood 40°38'48"N 73°53'54"W approx. 727, East 101st Street, Brooklyn, Kings County, City of New York, New York, 11236, United States Precinct Margin: D+92%	Voter 102's Neighborhood 34°44'33"N 86°43'35"W approx. 104, Stoneridge Circle, Stone Ridge, Madison, Madison County, Alabama, 35758, United States Precinct Margin: R+28%
Voter 103's Neighborhood 33°34'14"N 111°45'38"W approx. 9223, North Crown Ridge, Fountain Hills, Maricopa County, Arizona, 85268, United States Precinct Margin: R+25%	Voter 104's Neighborhood 44°9'44"N 92°10'22"W approx. 258, 5th Street Southwest, Plainview, Wabasha County, Minnesota, 55964, United States Precinct Margin: R+38%
Voter 105's Neighborhood 33°6'47"N 117°19'14"W approx. Avenida Encinas, Carlsbad, San Diego County, California, 92009-1114, United States Precinct Margin: D+18%	Voter 106's Neighborhood 33°44'29"N 118°20'40"W approx. Mariposa Trail, Rancho Palos Verdes, Los Angeles County, California, 90275, United States Precinct Margin: D+6%
Voter 107's Neighborhood 40°45'13"N 74°0'24"W approx. West 29th Street, Manhattan Community Board 4, Manhattan, New York County, City of New York, New York, 10001, United States Precinct Margin: D+75%	Voter 108's Neighborhood 37°41'50"N 113°3'4"W approx. 13th Hole Trail, Cedar City, Iron County, Utah, 83721, United States Precinct Margin: R+53%
Voter 109's Neighborhood 34°42'40"N 87°6'30"W approx. 11744, Nuclear Plant Road, Browns Ferry Nuclear Power Plant, Limestone County, Alabama, 35611, United States Precinct Margin: R+35%	Voter 110's Neighborhood 34°15'35"N 85°9'48"W approx. 168, Griffin Street, Hell's Hollow, Rome, Floyd County, Georgia, 30161, United States Precinct Margin: R+2%
Voter 111's Neighborhood 33°57'36"N 118°9'32"W approx. 6032, Gotham Street, Bell Gardens, Los Angeles County, California, 90201, United States Precinct Margin: D+66%	Voter 112's Neighborhood 43°8'6"N 77°32'17"W approx. 2615, East Avenue, Town/Village of East Rochester, Monroe County, New York, 14610, United States Precinct Margin: D+30%
Voter 113's Neighborhood 40°50'5"N 74°5'45"W approx. 278, Garden Street, East Rutherford, Bergen County, New Jersey, 07073, United States Precinct Margin: D+11%	Voter 114's Neighborhood 29°23'43"N 98°43'54"W approx. Mulberry Creek, Stoney Creek, Bexar County, Texas, United States Precinct Margin: D+17%
Voter 115's Neighborhood 41°20'1"N 73°47'7"W approx. 3686, Curry Street, Jefferson Valley, Jefferson Valley-Yorktown, Westchester County, New York, 10598, United States Precinct Margin: R+9%	Voter 116's Neighborhood 41°53'20"N 72°55'6"W approx. 296, Barbourtown Road, Canton, Hartford County, Connecticut, 06019, United States Precinct Margin: D+18%
Voter 117's Neighborhood 29°48'19"N 95°23'52"W approx. Hamilton Middle School, East 21st Street, Houston, Harris County, Texas, 77008, United States Precinct Margin: D+38%	Voter 118's Neighborhood 35°9'31"N 89°59'56"W approx. 765, Hawthorne Street, Memphis, Shelby County, Tennessee, 38107, United States Precinct Margin: D+63%
Voter 119's Neighborhood 26°14'4"N 81°40'47"W approx. 3472, 3rd Avenue Northwest, Golden Gate Estates, Collier County, Florida, 34120, United States Precinct Margin: R+34%	Voter 120's Neighborhood 39°20'49"N 76°47'57"W approx. 9041, Old Court Road, Randallstown, Baltimore County, Maryland, 21244, United States Precinct Margin: D+81%
Voter 121's Neighborhood 39°23'28"N 84°21'40"W approx. 7983, Princeton Road, The Trails of Four Bridges, Jericho, Liberty Township, Butler County, Ohio, 45044, United States Precinct Margin: R+26%	Voter 122's Neighborhood 25°45'21"N 80°13'8"W approx. 1435, Southwest 18th Street, Shenandoah, Miami, Miami-Dade County, Florida, 33145, United States Precinct Margin: R+2%
Voter 123's Neighborhood 38°55'53"N 77°1'25"W approx. 3318, Georgia Avenue Northwest, Pleasant Plains, Washington, District of Columbia, 20012, United States Precinct Margin: D+90%	Voter 124's Neighborhood 32°50'10"N 116°56'17"W approx. 8749, Almond Road, Winter Gardens, Lakeside, San Diego County, California, 92040, United States Precinct Margin: R+27%
Voter 125's Neighborhood 33°38'56"N 112°17'27"W approx. Willowbrook Golf Course, 10600, North Boswell Boulevard, Sun City, Maricopa County, Arizona, 85373, United States Precinct Margin: R+23%	Voter 126's Neighborhood 40°27'5"N 86°7'40"W approx. 3101, South Washington Street, Kokomo, Howard County, Indiana, 46902, United States Precinct Margin: R+23%
Voter 127's Neighborhood 44°1'29"N 88°32'23"W approx. 205, West Irving Avenue, Middle Village, Oshkosh, Winnebago County, Wisconsin, 54901, United States Precinct Margin: D+25%	Voter 128's Neighborhood 45°23'25"N 122°46'13"W approx. Tualatin Country Club, Tualatin River Trail, Cook Park, Tigard, Washington County, Oregon, 97062, United States Precinct Margin: D+35%
Voter 129's Neighborhood 36°13'46"N 121°7'44"W approx. Metz Road, King City, Monterey County, California, 93930, United States Precinct Margin: D+37%	Voter 130's Neighborhood 63°25'2"N 157°40'18"W approx. Unorganized Borough, Alaska, United States Precinct Margin: D+22%
Voter 131's Neighborhood 39°52'57"N 75°21'39"W approx. 88, Medbury Road, Avendale, Nether Providence Township, Delaware County, Pennsylvania, 19086, United States Precinct Margin: D+28%	Voter 132's Neighborhood 41°25'20"N 87°36'28"W approx. 1679, South State Street, Crete, Will County, Illinois, 60417, United States Precinct Margin: R+19%
Voter 133's Neighborhood 33°59'8"N 118°5'33"W approx. 6530, Bequette Avenue, Pico Rivera, Los Angeles County, California, 90660, United States Precinct Margin: D+57%	Voter 134's Neighborhood 21°20'9"N 158°4'26"W approx. Archery Center, Fort Barrette Road, City Center, Makakilo City, Kapolei, Honolulu County, Hawaii, 96707, United States Precinct Margin: D+9%
Voter 135's Neighborhood 33°48'30"N 84°46'25"W approx. 676, Timber Ridge Trail, Paulding County, Georgia, 30141, United States Precinct Margin: D+1%	Voter 136's Neighborhood 36°33'9"N 84°31'12"W approx. Grape Ruff Road, Scott County, Tennessee, 37841, United States Precinct Margin: R+76%
Voter 137's Neighborhood 33°56'37"N 118°20'50"W approx. West 102nd Street, Inglewood, Los Angeles County, California, 90304, United States Precinct Margin: D+66%	Voter 138's Neighborhood 41°0'0"N 74°21'5"W approx. 27, Western Avenue, Butler, Morris County, New Jersey, 07405, United States Precinct Margin: R+12%
Voter 139's Neighborhood 41°9'58"N 111°56'10"W approx. 1600, Mohawk Lane, Ogden, Weber County, Utah, 84403, United States Precinct Margin: R+19%	Voter 140's Neighborhood 45°38'48"N 122°39'26"W approx. 3505, N Street, Rose Village, Vancouver, Clark County, Washington, 98663, United States Precinct Margin: D+38%
Voter 141's Neighborhood 41°26'58"N 81°41'45"W approx. 3888, West 20th Street, Brooklyn Centre, Cleveland, Cuyahoga County, Ohio, 44109, United States Precinct Margin: D+29%	Voter 142's Neighborhood 41°16'47"N 87°48'41"W approx. 3425, East 11000N Road, Kankakee County, Illinois, 60468, United States Precinct Margin: R+35%
Voter 143's Neighborhood 40°2'46"N 75°4'35"W approx. 1260, Knorr Street, Lawndale, Philadelphia, Philadelphia County, Pennsylvania, 19149, United States Precinct Margin: D+63%	Voter 144's Neighborhood 41°45'31"N 86°4'44"W approx. 50541, Little John Lane, Sherwood Forest Estates, Granger, Saint Joseph County, Indiana, 46530, United States Precinct Margin: R+10%
Voter 145's Neighborhood 36°58'22"N 121°58'34"W approx. 2523, Harper Street, Yacht Harbor Manor, Twin Lakes, Santa Cruz County, California, 95062, United States Precinct Margin: D+62%	Voter 146's Neighborhood 45°46'47"N 115°12'20"W approx. Butter Creek Road, Idaho County, Idaho, United States Precinct Margin: R+74%
Voter 147's Neighborhood 32°40'40"N 97°22'15"W approx. 4733, Melita Avenue, Fort Worth, Tarrant County, Texas, 76133, United States Precinct Margin: D+14%	Voter 148's Neighborhood 41°27'56"N 87°4'20"W approx. Factory Street, Valparaiso, Porter County, Indiana, 46385, United States Precinct Margin: R+3%
Voter 149's Neighborhood 37°46'43"N 122°24'19"W approx. SOMA Pilipinas - Filipino Cultural Heritage District, 3rd Street, Union Square, San Francisco, California, 94107, United States Precinct Margin: D+80%	Voter 150's Neighborhood 47°40'48"N 117°21'23"W approx. 2451, North Sycamore Street, Minnehaha, Spokane, Spokane County, Washington, 99217, United States Precinct Margin: R+16%
Voter 151's Neighborhood 41°30'34"N 90°31'58"W approx. Great River Trail, Rock Island, Rock Island County, Illinois, 61299, United States Precinct Margin: D+43%	Voter 152's Neighborhood 42°24'8"N 83°45'20"W approx. 8000, Park Road, Northfield Township, Washtenaw County, Michigan, 48189, United States Precinct Margin: D+6%
Voter 153's Neighborhood 44°57'10"N 92°42'48"W approx. Hanley Road, Hudson, Saint Croix County, Wisconsin, 54016, United States Precinct Margin: R+0%	Voter 154's Neighborhood 39°43'53"N 121°51'25"W approx. 948, West Sacramento Avenue, Chico, Butte County, California, 95926, United States Precinct Margin: D+62%
Voter 155's Neighborhood 34°0'51"N 117°33'55"W approx. 3987, Bethany Way, Ontario, San Bernardino County, California, 91761, United States Precinct Margin: D+20%	Voter 156's Neighborhood 27°55'11"N 82°47'7"W approx. Largo Senior High School, 2nd Avenue Northeast, Largo, Pinellas County, Florida, 33770, United States Precinct Margin: R+3%
Voter 157's Neighborhood 40°45'5"N 96°42'57"W approx. Wilderness Park Hiker Trail, Lincoln, Lancaster County, Nebraska, 68512, United States Precinct Margin: D+4%	Voter 158's Neighborhood 40°38'54"N 73°42'51"W approx. 287, Hungry Harbor Road, Village of Valley Stream, Town of Hempstead, Nassau County, New York, 11581, United States Precinct Margin: D+17%
Voter 159's Neighborhood 35°8'28"N 80°46'0"W approx. Cottonwood Nature Trail, Olde Heritage, Charlotte, Mecklenburg County, North Carolina, 28270, United States Precinct Margin: D+33%	Voter 160's Neighborhood 30°46'23"N 87°25'29"W approx. 9935, Pilgrim Trail, Escambia County, Florida, 32577, United States Precinct Margin: R+69%
Voter 161's Neighborhood 40°42'45"N 73°50'51"W approx. 71-42, Kessel Street, Parkside, Queens, City of New York, New York, 11375, United States Precinct Margin: D+42%	Voter 162's Neighborhood 34°6'42"N 80°54'59"W approx. 2061, Bermuda Hills Road, Richland County, South Carolina, 29223, United States Precinct Margin: D+28%
Voter 163's Neighborhood 38°50'37"N 76°50'25"W approx. 3126, Squire Road, Westphalia Estates, Upper Marlboro, Prince George's County, Maryland, 20772, United States Precinct Margin: D+89%	Voter 164's Neighborhood 32°33'0"N 82°56'31"W approx. Ridge Circle, Dublin, Laurens County, Georgia, 31021, United States Precinct Margin: R+25%
Voter 165's Neighborhood 33°22'52"N 111°32'25"W approx. 546, East 37th Avenue, Apache Junction, Pinal County, Arizona, 85119, United States Precinct Margin: R+24%	Voter 166's Neighborhood 44°4'7"N 121°17'59"W approx. 456, Northeast Seward Avenue, Bend, Deschutes County, Oregon, 97701, United States Precinct Margin: D+30%
Voter 167's Neighborhood 41°34'36"N 87°19'3"W approx. 2232, Mississippi Street, Pulaski, Gary, Lake County, Indiana, 46407, United States Precinct Margin: D+92%	Voter 168's Neighborhood 33°24'38"N 111°43'24"W approx. 498, East Boeing, Venture Out, Gilbert, Mesa, Maricopa County, Arizona, 85205, United States Precinct Margin: R+14%
Voter 169's Neighborhood 40°51'44"N 73°55'46"W approx. 2, Sherman Avenue, Fort George, Manhattan, New York County, City of New York, New York, 10040, United States Precinct Margin: D+75%	Voter 170's Neighborhood 42°17'59"N 88°24'14"W approx. Bentgrass Lane, Woodstock, McHenry County, Illinois, 60098, United States Precinct Margin: R+8%
Voter 171's Neighborhood 35°21'17"N 119°0'59"W approx. 91, L Street, Civic Center, Bakersfield, Kern County, California, 93304, United States Precinct Margin: D+55%	Voter 172's Neighborhood 28°21'53"N 82°41'17"W approx. 7644, Andrews Street, Club Wildwood, Hudson, Pasco County, Florida, 34667, United States Precinct Margin: R+30%
Voter 173's Neighborhood 32°47'16"N 96°52'21"W approx. 3804, Delhi Street, Dallas, Dallas County, Texas, 75212, United States Precinct Margin: D+80%	Voter 174's Neighborhood 44°0'16"N 91°26'13"W approx. 24258, Great River Road, Trempealeau, Trempealeau County, Wisconsin, 54661, United States Precinct Margin: R+9%
Voter 175's Neighborhood 30°28'31"N 91°8'37"W approx. 2989, Addison Street, Belfair, Prescott Place, Baton Rouge, East Baton Rouge Parish, Louisiana, 70805, United States Precinct Margin: D+91%	Voter 176's Neighborhood 40°19'42"N 79°44'13"W approx. Circleville School Site (Historic), Robbins Station Road, Cedar Glenn, Circleville, North Huntingdon Township, Westmoreland County, Pennsylvania, 15642, United States Precinct Margin: R+32%
Voter 177's Neighborhood 35°6'33"N 106°31'4"W approx. Walmart Pharmacy, Paseo de las Montañas Trail, Casa Grande/South Glenwood Hills, Enchanted Park, Albuquerque, Bernalillo County, New Mexico, 87184, United States Precinct Margin: D+23%	Voter 178's Neighborhood 39°11'37"N 77°12'23"W approx. 20617, Bell Bluff Road, Prathertown, Montgomery Village, Montgomery County, Maryland, 20879, United States Precinct Margin: D+56%
Voter 179's Neighborhood 33°34'14"N 112°6'33"W approx. 9228, North 23rd Avenue, Phoenix, Maricopa County, Arizona, 85021, United States Precinct Margin: D+25%	Voter 180's Neighborhood 26°14'4"N 81°40'47"W approx. 3472, 3rd Avenue Northwest, Golden Gate Estates, Collier County, Florida, 34120, United States Precinct Margin: R+34%
Voter 181's Neighborhood 39°15'18"N 74°45'35"W approx. Mt Pleasant - Tuckahoe Road, Tuckahoe, Upper Township, Cape May County, New Jersey, 08270, United States Precinct Margin: R+19%	Voter 182's Neighborhood 29°46'40"N 95°47'13"W approx. 23802, North Newport Bend, Harris County, Texas, 77494, United States Precinct Margin: R+7%
Voter 183's Neighborhood 27°55'3"N 82°29'59"W approx. 3464, West San Pedro Street, Palma Ceia, Tampa, Hillsborough County, Florida, 33629, United States Precinct Margin: D+12%	Voter 184's Neighborhood 42°26'14"N 92°19'2"W approx. 5391, Hess Road, Waterloo, Black Hawk County, Iowa, 50701, United States Precinct Margin: D+7%
Voter 185's Neighborhood 44°53'43"N 93°21'35"W approx. 5318, West 60th Street, Edina, Hennepin County, Minnesota, 55436, United States Precinct Margin: D+35%	Voter 186's Neighborhood 42°47'46"N 83°14'26"W approx. 998, Wildbrook Lane, Oakland County, Michigan, 48362, United States Precinct Margin: R+14%
Voter 187's Neighborhood 40°56'33"N 74°4'40"W approx. The Ridgewood Country Club, 96, West Midland Avenue, Paramus, Bergen County, New Jersey, 07652, United States Precinct Margin: R+1%	Voter 188's Neighborhood 35°46'49"N 84°2'3"W approx. 765, Hi View Lane, Blount County, Tennessee, 37801, United States Precinct Margin: R+49%
Voter 189's Neighborhood 44°43'17"N 93°26'12"W approx. 4116, Grainwood Circle Northeast, Grainwood, Prior Lake, Scott County, Minnesota, 55372, United States Precinct Margin: R+9%	Voter 190's Neighborhood 45°28'44"N 122°29'31"W approx. 5989, Southeast Jenne Lane, Pleasant Valley, Portland, Multnomah County, Oregon, 97236, United States Precinct Margin: D+18%
Voter 191's Neighborhood 46°50'16"N 96°44'55"W approx. 36th Avenue South, Moorhead, Clay County, Minnesota, 56560, United States Precinct Margin: D+12%	Voter 192's Neighborhood 29°37'11"N 98°31'43"W approx. 1678, Greystone Ridge, San Antonio, Bexar County, Texas, 78258, United States Precinct Margin: R+8%
Voter 193's Neighborhood 42°25'22"N 71°4'14"W approx. 66;80, Charles Street, Malden Centre, Malden, Middlesex County, Massachusetts, 02148, United States Precinct Margin: D+65%	Voter 194's Neighborhood 39°56'40"N 82°50'41"W approx. Yorktown Middle School, Red Apple Ridge Road, Columbus, Franklin County, Ohio, 43068-3983, United States Precinct Margin: D+57%
Voter 195's Neighborhood 38°42'47"N 90°17'30"W approx. 7341, Wallington Walk, Norwood Court Apartments, Norwood Court, Saint Louis County, Missouri, 63121, United States Precinct Margin: D+89%	Voter 196's Neighborhood 32°24'26"N 96°51'10"W approx. Sheaffer Full Life Center, Savell Circle, Waxahachie, Ellis County, Texas, 75165, United States Precinct Margin: R+37%
Voter 197's Neighborhood 40°44'16"N 74°13'14"W approx. Munn Avenue, Irvington, Essex County, New Jersey, 07018:07052, United States Precinct Margin: D+90%	Voter 198's Neighborhood 41°41'56"N 77°35'27"W approx. 10121, Leetonia Road, Tioga County, Pennsylvania, 16921, United States Precinct Margin: R+53%
Voter 199's Neighborhood 34°45'41"N 92°25'16"W approx. 56, Perdido Circle, Saint Charles, Little Rock, Pulaski County, Arkansas, 72211, United States Precinct Margin: D+26%	Voter 200's Neighborhood 36°17'51"N 80°20'27"W approx. 395, Hartgrove Road, Stokes County, North Carolina, 27021, United States Precinct Margin: R+54%
Voter 201's Neighborhood 39°38'57"N 105°4'45"W approx. Comfort Inn & Suites, West Jefferson Avenue, Lakewood, Jefferson County, Colorado, 80235, United States Precinct Margin: D+25%	Voter 202's Neighborhood 36°8'27"N 83°51'48"W approx. 7954, Lett Road, Knox County, Tennessee, 37721, United States Precinct Margin: R+60%
Voter 203's Neighborhood 29°6'39"N 82°13'11"W approx. Southwest 61st Avenue, Marion County, Florida, 34476, United States Precinct Margin: R+21%	Voter 204's Neighborhood 41°23'16"N 79°17'44"W approx. Rail 66 Country Trail, Roses, Jenks Township, Forest County, Pennsylvania, 16239, United States Precinct Margin: R+52%
Voter 205's Neighborhood 40°51'47"N 73°49'15"W approx. 120, Elgar Place, Bronx County, The Bronx, City of New York, New York, 10475, United States Precinct Margin: D+84%	Voter 206's Neighborhood 35°3'20"N 106°31'55"W approx. Analytical Solutions Incorporated, 10401, Research Road Southeast, Albuquerque, Bernalillo County, New Mexico, 87123, United States Precinct Margin: D+22%
Voter 207's Neighborhood 43°5'27"N 89°21'31"W approx. 1875, East Main Street, Marquette, Madison, Dane County, Wisconsin, 53704, United States Precinct Margin: D+92%	Voter 208's Neighborhood 43°6'35"N 85°39'32"W approx. 7954, Krupp Avenue Northeast, Plainfield Charter Township, Kent County, Michigan, 49321, United States Precinct Margin: R+13%
Voter 209's Neighborhood 39°39'7"N 84°7'51"W approx. 449, Carters Grove Road, Oak Ridge, Centerville, Montgomery County, Ohio, 45459, United States Precinct Margin: D+10%	Voter 210's Neighborhood 41°24'39"N 72°8'18"W approx. Miller Pond Road, Waterford, New London County, Connecticut, 06375, United States Precinct Margin: D+18%
Voter 211's Neighborhood 35°2'7"N 78°16'31"W approx. 299, Capers Walk Lane, Sampson County, North Carolina, 28328, United States Precinct Margin: D+19%	Voter 212's Neighborhood 39°34'12"N 95°8'39"W approx. Atchison Elementary School, 825, North 17th Street, Atchison, Atchison County, Kansas, 66002, United States Precinct Margin: R+17%
Voter 213's Neighborhood 42°36'42"N 83°55'24"W approx. 752, North Barnard Street, Howell, Livingston County, Michigan, 48843, United States Precinct Margin: R+14%	Voter 214's Neighborhood 32°40'43"N 117°14'47"W approx. Point Loma Wastewater Treatment Plant, 1902, Lands End Road, San Diego, San Diego County, California, 92106, United States Precinct Margin: D+23%
Voter 215's Neighborhood 40°33'47"N 74°11'7"W approx. 83, Jamie Lane, Fresh Kills, Staten Island, City of New York, New York, 10312, United States Precinct Margin: R+11%	Voter 216's Neighborhood 40°25'49"N 79°54'51"W approx. Riverview Trail, Squirrel Hill South, Pittsburgh, Allegheny County, Pennsylvania, 15217, United States Precinct Margin: D+63%
Voter 217's Neighborhood 33°44'15"N 117°53'49"W approx. Monte Vista Elementary School, South Center Street, Santa Ana, Orange County, California, 92704, United States Precinct Margin: D+62%	Voter 218's Neighborhood 39°50'49"N 88°53'5"W approx. 483, Green Way Lane, Country Club, Decatur, Macon County, Illinois, 62521, United States Precinct Margin: R+17%
Voter 219's Neighborhood 40°19'55"N 76°28'9"W approx. 522, South Garfield Street, North Cornwall Township, Lebanon County, Pennsylvania, 17042, United States Precinct Margin: R+24%	Voter 220's Neighborhood 39°35'34"N 89°22'2"W approx. 1675, North 900 East Road, Christian County, Illinois, 62568, United States Precinct Margin: R+41%
Voter 221's Neighborhood 45°38'7"N 89°31'45"W approx. 6932, Beyer Road, Town of Crescent, Oneida County, Wisconsin, 54501, United States Precinct Margin: R+11%	Voter 222's Neighborhood 27°56'45"N 82°15'12"W approx. 2077, Florida Street, Valrico, Brandon, Hillsborough County, Florida, 33594, United States Precinct Margin: R+6%
Voter 223's Neighborhood 34°5'32"N 117°38'49"W approx. 8th Street, North Ontario, Upland, San Bernardino County, California, 91786, United States Precinct Margin: D+32%	Voter 224's Neighborhood 43°59'43"N 70°31'36"W approx. 136, Leach Hill Road, Casco Village, Casco, Cumberland County, Maine, 04015, United States Precinct Margin: R+6%
Voter 225's Neighborhood 29°39'38"N 95°40'45"W approx. 10592, Clodine Road, Sugar Land, Fort Bend County, Texas, 77469, United States Precinct Margin: D+24%	Voter 226's Neighborhood 40°41'30"N 111°51'39"W approx. 3655, Christine Street, Millcreek, Salt Lake County, Utah, 84106, United States Precinct Margin: D+47%
Voter 227's Neighborhood 33°53'1"N 117°51'3"W approx. 1256, Venice Avenue, Placentia, Orange County, California, 92870, United States Precinct Margin: R+6%	Voter 228's Neighborhood 34°59'27"N 85°16'2"W approx. 3661, Craig Street, Milbro Heights, East Ridge, Hamilton County, Tennessee, 37412, United States Precinct Margin: R+14%
Voter 229's Neighborhood 33°17'55"N 111°45'32"W approx. 1443, East Joseph Way, The Spectrum at Val Vista, Gilbert, Maricopa County, Arizona, 85295, United States Precinct Margin: R+8%	Voter 230's Neighborhood 35°11'55"N 85°9'33"W approx. Food City, McConnell School Lane, Lakesite, Hamilton County, Tennessee, 37379, United States Precinct Margin: R+53%
Voter 231's Neighborhood 33°49'30"N 117°47'12"W approx. 6363, East Blairwood Lane, Orange, Orange County, California, 92867, United States Precinct Margin: R+12%	Voter 232's Neighborhood 33°48'25"N 117°50'44"W approx. 774, East Wilson Avenue, Orange, Orange County, California, 92867, United States Precinct Margin: D+5%
Voter 233's Neighborhood 28°8'51"N 81°50'55"W approx. Florida Polytechnic University, 4700, Research Way, Lakeland, Polk County, Florida, 33805-8531, United States Precinct Margin: R+19%	Voter 234's Neighborhood 35°56'9"N 84°6'7"W approx. 804, Chateaugay Road, Gulf Park-Belmont West-Plum Creek, Cedar Bluff, Knox County, Tennessee, 37923, United States Precinct Margin: R+6%
Voter 235's Neighborhood 32°20'12"N 99°34'45"W approx. 6950, County Road 223, Callahan County, Texas, 79510, United States Precinct Margin: R+77%	Voter 236's Neighborhood 38°17'37"N 85°57'20"W approx. Georgetown Lake, Baylor Wissman Road, Georgetown, Floyd County, Indiana, 47122, United States Precinct Margin: R+21%
Voter 237's Neighborhood 61°11'36"N 149°51'3"W approx. 2984, Madison Way, College Village, Anchorage, Alaska, 99508, Anchorage Precinct Margin: D+25%	Voter 238's Neighborhood 39°38'55"N 104°44'24"W approx. 3601, S Nepal Street, Aurora, Arapahoe County, Colorado, 80013, United States Precinct Margin: D+18%
Voter 239's Neighborhood 38°23'47"N 121°26'42"W approx. 5080, Orchid Ranch Way, Elk Grove, Sacramento County, California, 95757, United States Precinct Margin: D+36%	Voter 240's Neighborhood 36°55'37"N 121°45'7"W approx. T S MacQuiddy Elementary School, Martinelli Street, Watsonville, Santa Cruz County, California, 95076, United States Precinct Margin: D+54%
Voter 241's Neighborhood 33°35'13"N 84°37'12"W approx. Nathaniel Lane, Fulton County, Georgia, 30213, United States Precinct Margin: D+91%	Voter 242's Neighborhood 40°45'57"N 96°41'41"W approx. 1899, Center Park Road, Lincoln, Lancaster County, Nebraska, 68512, United States Precinct Margin: D+20%
Voter 243's Neighborhood 38°47'34"N 90°41'41"W approx. Dude's Way, O’Fallon, Saint Charles County, Missouri, 63366, United States Precinct Margin: R+9%	Voter 244's Neighborhood 32°44'28"N 96°46'32"W approx. 1020, Sargent Road, Sargent, Dallas, Dallas County, Texas, 75203, United States Precinct Margin: D+85%
Voter 245's Neighborhood 33°36'27"N 117°11'29"W approx. 26761, Chamomile Street, Greer Ranch, Murrieta, Riverside County, California, 92562, United States Precinct Margin: R+22%	Voter 246's Neighborhood 35°25'46"N 119°1'38"W approx. North High School, Galaxy Avenue, Kern County, California, 93301, United States Precinct Margin: R+53%
Voter 247's Neighborhood 40°2'0"N 75°4'30"W approx. 1901, Lardner Street, Philadelphia, Philadelphia County, Pennsylvania, 19149, United States Precinct Margin: D+55%	Voter 248's Neighborhood 41°40'32"N 72°20'2"W approx. 26, Hunt Road, Columbia, Tolland County, Connecticut, 06237, United States Precinct Margin: D+8%
Voter 249's Neighborhood 41°16'35"N 72°36'5"W approx. Island Avenue Elementary School, 20, Island Avenue, Madison, New Haven County, Connecticut, 06443, United States Precinct Margin: D+27%	Voter 250's Neighborhood 41°43'45"N 83°38'45"W approx. Pelton Lane, Bedford Township, Monroe County, Michigan, 49267, United States Precinct Margin: R+12%
Voter 251's Neighborhood 42°22'30"N 71°3'47"W approx. 8, Cordis Street, Charlestown, Boston, Suffolk County, Massachusetts, 02129, United States Precinct Margin: D+65%	Voter 252's Neighborhood 34°38'43"N 86°28'20"W approx. Hays Preserve Trail, Huntsville, Madison County, Alabama, 35763, United States Precinct Margin: R+40%
Voter 253's Neighborhood 36°2'34"N 86°39'42"W approx. 5333, Cane Ridge Road, Bell Hollow Apartments, Nashville-Davidson, Davidson County, Tennessee, 37013, United States Precinct Margin: D+55%	Voter 254's Neighborhood 39°36'13"N 119°47'13"W approx. 291, Harmony Lane, Sun Valley, Washoe County, Nevada, 89433, United States Precinct Margin: D+15%
Voter 255's Neighborhood 42°39'25"N 71°19'56"W approx. 274;276, University Avenue, Pawtucketville, Lowell, Middlesex County, Massachusetts, 01854-5141, United States Precinct Margin: D+33%	Voter 256's Neighborhood 40°21'9"N 76°8'21"W approx. 228, West Oak Avenue, Robesonia, Berks County, Pennsylvania, 19551, United States Precinct Margin: R+26%
Voter 257's Neighborhood 42°34'56"N 73°49'1"W approx. 79, Crescent Creek Way, Dutch Mills, Town of Bethlehem, Albany County, New York, 12158, United States Precinct Margin: D+36%	Voter 258's Neighborhood 40°14'50"N 80°9'51"W approx. 117, Fulton Road, Hill Church, North Strabane Township, Washington County, Pennsylvania, 15317, United States Precinct Margin: R+19%
Voter 259's Neighborhood 25°46'46"N 80°20'46"W approx. 1016, Northwest 87th Avenue, Miami-Dade County, Florida, 33172, United States Precinct Margin: R+3%	Voter 260's Neighborhood 42°54'42"N 87°52'27"W approx. 1640, Monroe Avenue, South Milwaukee, Milwaukee County, Wisconsin, 53172, United States Precinct Margin: D+0%
Voter 261's Neighborhood 36°4'31"N 115°18'11"W approx. 9714, Hawk Cliff Avenue, Spinnaker at Southwest Ranch, Spring Valley, Clark County, Nevada, 89148, United States Precinct Margin: D+23%	Voter 262's Neighborhood 42°36'42"N 83°20'44"W approx. 1849, Cass Lake Front Street, Keego Harbor, Oakland County, Michigan, 48320, United States Precinct Margin: D+5%
Voter 263's Neighborhood 44°58'35"N 123°4'25"W approx. 2943, Wallace Road Northwest, Salemtowne, Salem, Polk County, Oregon, 97304, United States Precinct Margin: D+9%	Voter 264's Neighborhood 44°58'50"N 122°49'36"W approx. 11417, Evergreen Road Northeast, Marion County, Oregon, 97381, United States Precinct Margin: R+31%
Voter 265's Neighborhood 46°43'13"N 92°27'26"W approx. 34, 6th Street, Cloquet, Carlton County, Minnesota, 55720, United States Precinct Margin: D+11%	Voter 266's Neighborhood 40°52'20"N 117°44'46"W approx. 4746, Tycana Road, Humboldt County, Nevada, 89445, United States Precinct Margin: R+71%
Voter 267's Neighborhood 27°56'1"N 82°28'30"W approx. 1539, West Morrison Avenue, Historic Hyde Park North Neighborhood, Hyde Park, Tampa, Hillsborough County, Florida, 33606, United States Precinct Margin: D+14%	Voter 268's Neighborhood 44°59'54"N 91°43'39"W approx. Colfax Pharmacy, River Street, Colfax, Dunn County, Wisconsin, 54730, United States Precinct Margin: R+5%
Voter 269's Neighborhood 38°34'58"N 90°22'4"W approx. 422, Somerset Avenue, Sherwood Forest, Webster Groves, Saint Louis County, Missouri, 63119, United States Precinct Margin: D+43%	Voter 270's Neighborhood 34°8'42"N 82°58'58"W approx. Hughes Road, Elbert County, Georgia, 30634, United States Precinct Margin: R+26%
Voter 271's Neighborhood 39°23'30"N 76°34'2"W approx. 1664, Thetford Road, Knettishall, Towson, Baltimore County, Maryland, 21286, United States Precinct Margin: D+51%	Voter 272's Neighborhood 41°42'40"N 79°50'14"W approx. 35284, Armstrong Road, Steuben Township, Crawford County, Pennsylvania, 16360, United States Precinct Margin: R+51%
Voter 273's Neighborhood 43°3'6"N 76°5'51"W approx. 636, Hazelwood Avenue, Salt Springs, City of Syracuse, Syracuse, Onondaga County, New York, 13224, United States Precinct Margin: D+82%	Voter 274's Neighborhood 42°52'21"N 87°59'40"W approx. 6482, West Ryan Road, Franklin, Milwaukee County, Wisconsin, 53132, United States Precinct Margin: R+7%
Voter 275's Neighborhood 42°47'30"N 71°6'10"W approx. 30, Bennington Street, Haverhill, Essex County, Massachusetts, 01832, United States Precinct Margin: D+17%	Voter 276's Neighborhood 35°17'53"N 119°7'25"W approx. 6299, Long Valley Way, Bakersfield, Kern County, California, 93311, United States Precinct Margin: D+7%
Voter 277's Neighborhood 25°57'46"N 97°34'14"W approx. Carmen Avenue, Brownsville, Cameron County, Texas, United States Precinct Margin: D+18%	Voter 278's Neighborhood 33°41'40"N 86°16'6"W approx. 129, Turkey Ridge Road, St. Clair County, Alabama, 35131, United States Precinct Margin: R+81%
Voter 279's Neighborhood 44°59'12"N 92°58'28"W approx. 2619, Granada Avenue North, Oakdale, Washington County, Minnesota, 55128, United States Precinct Margin: D+17%	Voter 280's Neighborhood 37°32'6"N 77°17'44"W approx. 1729, Casey Meadows Terrace, Forest Meadow Mobile Home Park, Henrico County, Virginia, 23150, United States Precinct Margin: D+38%
Voter 281's Neighborhood 37°24'54"N 77°47'57"W approx. 6211, Clayville Lane, Chesterfield County, Virginia, 23120, United States Precinct Margin: R+19%	Voter 282's Neighborhood 43°14'1"N 86°11'49"W approx. Popeyes, Gordon Street, Shady Park Neighbourhood, Muskegon Township, Muskegon County, Michigan, 49442, United States Precinct Margin: D+6%
Voter 283's Neighborhood 42°27'25"N 83°12'31"W approx. 16225, Roanoke Street, Southfield, Oakland County, Michigan, 48075, United States Precinct Margin: D+89%	Voter 284's Neighborhood 29°57'45"N 90°15'33"W approx. Moss Lane, Jefferson Parish, Louisiana, 70094, United States Precinct Margin: D+23%
Voter 285's Neighborhood 39°47'3"N 104°50'47"W approx. 12150, East 48th Avenue, Montbello, Denver, Colorado, 80239, United States Precinct Margin: D+77%	Voter 286's Neighborhood 39°50'37"N 80°35'2"W approx. 129, Grave Creek Road, Loudenville, Marshall County, West Virginia, 26033, United States Precinct Margin: R+83%
Voter 287's Neighborhood 34°16'36"N 118°40'41"W approx. 5808, East Malton Avenue, White Oak, Simi Valley, Ventura County, California, 93063, United States Precinct Margin: D+5%	Voter 288's Neighborhood 44°20'52"N 103°46'51"W approx. 656, Hearst Avenue, Lead, Lawrence County, South Dakota, 57754, United States Precinct Margin: R+9%
Voter 289's Neighborhood 33°47'49"N 84°11'56"W approx. 4614, Hairston Crossing Place, DeKalb County, Georgia, 30083, United States Precinct Margin: D+82%	Voter 290's Neighborhood 26°1'46"N 80°9'47"W approx. 2700, Scott Street, Hollywood, Broward County, Florida, 33020, United States Precinct Margin: D+17%
Voter 291's Neighborhood 28°41'26"N 81°36'33"W approx. Lake Apopka Wildlife Drive (Laughlin Road), Orange County, Florida, 34778, United States Precinct Margin: D+29%	Voter 292's Neighborhood 40°44'4"N 73°6'47"W approx. 103, Matthews Road, West Sayville, Suffolk County, New York, 11769, United States Precinct Margin: R+16%
Voter 293's Neighborhood 30°34'36"N 90°55'11"W approx. 10354, D Taylor Street, Livingston Parish, Louisiana, 70706, United States Precinct Margin: R+75%	Voter 294's Neighborhood 34°6'43"N 84°27'44"W approx. 1606, Barnes Road, Woodstock, Cherokee County, Georgia, 30188, United States Precinct Margin: R+23%
Voter 295's Neighborhood 40°37'3"N 74°24'45"W approx. 318, Franklin Place, Plainfield, Union County, New Jersey, 07060, United States Precinct Margin: D+74%	Voter 296's Neighborhood 40°26'41"N 99°22'10"W approx. 1076, East Avenue, Westside Plaza Mobile Home Park, Holdrege, Phelps County, Nebraska, 68949, United States Precinct Margin: R+55%
Voter 297's Neighborhood 26°6'36"N 80°7'45"W approx. 1032, Southeast 13th Terrace, Lauderdale Harbors, Fort Lauderdale, Broward County, Florida, 33316, United States Precinct Margin: R+8%	Voter 298's Neighborhood 35°55'55"N 94°11'6"W approx. 25, Riverwood Avenue, West Fork, Washington County, Arkansas, 72774, United States Precinct Margin: R+26%
Voter 299's Neighborhood 40°50'31"N 73°59'3"W approx. 1235, 15th Street, Fort Lee, Bergen County, New Jersey, 07024, United States Precinct Margin: D+26%	Voter 300's Neighborhood 36°25'56"N 77°38'46"W approx. 250, Smith Church Road, Roanoke Rapids, Halifax County, North Carolina, 27870, United States Precinct Margin: R+16%
Voter 301's Neighborhood 42°35'52"N 73°49'54"W approx. 801, Feura Bush Road, Houcks Corners, Town of Bethlehem, Albany County, New York, 12054, United States Precinct Margin: D+40%	Voter 302's Neighborhood 40°46'45"N 97°3'24"W approx. 404, Cottonwood Avenue, Milford, Seward County, Nebraska, 68405, United States Precinct Margin: R+47%
Voter 303's Neighborhood 26°13'20"N 98°5'54"W approx. 217, East Nolana Loop, Arriaga Colonia, Hidalgo County, Texas, 78516, United States Precinct Margin: D+31%	Voter 304's Neighborhood 36°7'30"N 115°16'18"W approx. Desert Breeze Community Center, West Spring Mountain Road, Spring Valley, Clark County, Nevada, 89147, United States Precinct Margin: D+8%
Voter 305's Neighborhood 39°1'22"N 77°2'22"W approx. 10323, Green Holly Terrace, Northbrook Estates, Forest Estates, Wheaton, Montgomery County, Maryland, 20902, United States Precinct Margin: D+73%	Voter 306's Neighborhood 41°47'34"N 87°39'31"W approx. 5528, South Ada Street, West Englewood, Chicago, Lake Township, Cook County, Illinois, 60636, United States Precinct Margin: D+91%
Voter 307's Neighborhood 40°46'57"N 73°10'34"W approx. 94, Sportsmen Street, Suffolk County, New York, 11722, United States Precinct Margin: D+20%	Voter 308's Neighborhood 41°8'31"N 81°46'29"W approx. 4832, Boneta Road, Granger Township, Medina County, Ohio, 44256, United States Precinct Margin: R+37%
Voter 309's Neighborhood 34°3'50"N 80°59'1"W approx. Sunglow Lane, Richland County, South Carolina, 29223, United States Precinct Margin: D+83%	Voter 310's Neighborhood 40°23'55"N 91°22'15"W approx. Keokuk Power Plant, Orleans Avenue, Keokuk, Lee County, Iowa, 52632, United States Precinct Margin: R+25%
Voter 311's Neighborhood 47°39'20"N 122°21'29"W approx. 120, Northwest 40th Street, Fremont, Seattle, King County, Washington, 98107, United States Precinct Margin: D+86%	Voter 312's Neighborhood 34°4'6"N 84°37'31"W approx. 4767, Webster Way Northwest, Baker Ridge, Cobb County, Georgia, 30101, United States Precinct Margin: D+20%
Voter 313's Neighborhood 42°25'38"N 71°14'13"W approx. Hayden Woods, Valleyfield Street, Lexington, Middlesex County, Massachusetts, 02421, United States Precinct Margin: D+68%	Voter 314's Neighborhood 33°29'19"N 101°55'8"W approx. 4998, 116th Street, Lubbock, Lubbock County, Texas, 79424, United States Precinct Margin: R+58%
Voter 315's Neighborhood 32°45'7"N 117°8'8"W approx. 2629, Polk Avenue, University Heights, North Park, San Diego, San Diego County, California, 92104, United States Precinct Margin: D+74%	Voter 316's Neighborhood 36°31'21"N 79°45'4"W approx. 900, Hilltop Lane, Eden, Rockingham County, North Carolina, 27288, United States Precinct Margin: R+22%
Voter 317's Neighborhood 37°55'43"N 122°18'54"W approx. 2034, Harper Street, El Cerrito, Contra Costa County, California, 94530, United States Precinct Margin: D+76%	Voter 318's Neighborhood 40°8'14"N 74°39'23"W approx. Chesterfield Elementary School, 30, Saddle Way, Villages at Chesterfield Greens, Chesterfield Township, Burlington County, New Jersey, 08515, United States Precinct Margin: D+6%
Voter 319's Neighborhood 33°24'15"N 111°46'25"W approx. Sun Circle Trail, Lindsay Crossing, Gilbert, Mesa, Maricopa County, Arizona, 85203, United States Precinct Margin: R+17%	Voter 320's Neighborhood 39°49'57"N 86°10'23"W approx. 4280, Crown Street, Mapleton, Indianapolis, Marion County, Indiana, 46208, United States Precinct Margin: D+71%
Voter 321's Neighborhood 38°52'22"N 77°12'43"W approx. 2824, Wickersham Way, West Falls Church, Fairfax County, Virginia, 22042, United States Precinct Margin: D+52%	Voter 322's Neighborhood 42°56'8"N 83°38'9"W approx. 10800, Walker Street, Grand Blanc, Genesee County, Michigan, 48439, United States Precinct Margin: D+7%
Voter 323's Neighborhood 28°17'54"N 81°39'52"W approx. 144, Kings Ridge Loop, The Ridge, Polk County, Florida, 33897, United States Precinct Margin: D+20%	Voter 324's Neighborhood 38°38'44"N 121°19'14"W approx. 4544, Onyx Way, Sacramento County, California, 95608, United States Precinct Margin: D+12%
Voter 325's Neighborhood 26°12'11"N 80°8'48"W approx. Cypress Creek Road, Fort Lauderdale, Broward County, Florida, 33334, United States Precinct Margin: D+20%	Voter 326's Neighborhood 32°31'53"N 92°12'0"W approx. 198, Davis Lane, Pine Grove, Ouachita Parish, Louisiana, 71291, United States Precinct Margin: R+73%
Voter 327's Neighborhood 41°28'34"N 87°29'2"W approx. 2557, Ticonderoga Street, Schererville, Lake County, Indiana, 46375, United States Precinct Margin: R+7%	Voter 328's Neighborhood 32°48'47"N 79°44'3"W approx. 31, Seagrass Lane, Isle of Palms, Charleston County, South Carolina, 29451, United States Precinct Margin: R+22%
Voter 329's Neighborhood 39°27'1"N 77°22'47"W approx. Liberty Road, Frederick, Frederick County, Maryland, 21701, United States Precinct Margin: D+34%	Voter 330's Neighborhood 34°46'33"N 102°57'15"W approx. 3435, County Road U, Deaf Smith County, Texas, 79035, United States Precinct Margin: R+61%
Voter 331's Neighborhood 40°32'54"N 105°5'7"W approx. Meadowlark Church of Christ, 2810, Meadowlark Avenue, Meadow Lark Heights, Fort Collins, Larimer County, Colorado, 80526, United States Precinct Margin: D+40%	Voter 332's Neighborhood 32°14'21"N 81°14'8"W approx. HiHo Hill, Coldbrook, Effingham County, Georgia, 31326, United States Precinct Margin: R+46%
Voter 333's Neighborhood 42°7'27"N 87°49'46"W approx. 2006, Illinois Road, Northbrook Park, Northbrook, Northfield Township, Cook County, Illinois, 60062, United States Precinct Margin: D+36%	Voter 334's Neighborhood 40°40'26"N 76°13'27"W approx. 2115, West Norwegian Street, Yorkville, Pottsville, Schuylkill County, Pennsylvania, 17901, United States Precinct Margin: D+0%
Voter 335's Neighborhood 40°32'32"N 80°11'17"W approx. 99, Linden Place, Sewickley, Allegheny County, Pennsylvania, 15143, United States Precinct Margin: D+19%	Voter 336's Neighborhood 41°30'37"N 81°25'40"W approx. 6601, Norvale Circle West, Gates Mills, Cuyahoga County, Ohio, 44040, United States Precinct Margin: D+1%
Voter 337's Neighborhood 40°43'9"N 80°8'41"W approx. Brush Creek Water Pollution Control Facility, 2306, Powell Road, Cranberry Township, Butler County, Pennsylvania, 16066, United States Precinct Margin: R+11%	Voter 338's Neighborhood 36°10'22"N 86°12'12"W approx. 3413, Eastover Road, Wilson County, Tennessee, 37184, United States Precinct Margin: R+57%
Voter 339's Neighborhood 40°3'9"N 105°18'40"W approx. 18, Pine Brook Road, Pine Brook Hill, Boulder County, Colorado, 80304, United States Precinct Margin: D+70%	Voter 340's Neighborhood 43°56'54"N 76°7'33"W approx. Battlefield History Trail, Sackets Harbor, Hounsfield, Jefferson County, New York, 13685, United States Precinct Margin: D+11%
Voter 341's Neighborhood 47°43'25"N 122°11'11"W approx. 13806, 116th Avenue Northeast, Kingsgate, Kirkland, King County, Washington, 98034, United States Precinct Margin: D+25%	Voter 342's Neighborhood 36°8'9"N 78°55'14"W approx. 7313, Johnson Mill Road, Durham County, North Carolina, 27503, United States Precinct Margin: D+4%
Voter 343's Neighborhood 42°26'15"N 83°21'11"W approx. Norfolk Street, Livonia, Wayne County, Michigan, 48152, United States Precinct Margin: D+10%	Voter 344's Neighborhood 39°32'45"N 74°45'8"W approx. Weymouth Elwood Road, Hamilton Township, Atlantic County, New Jersey, 08330, United States Precinct Margin: D+9%
Voter 345's Neighborhood 34°59'55"N 92°28'35"W approx. 527, Round Mountain Road, Round Mountain, Faulkner County, Arkansas, 72034, United States Precinct Margin: R+18%	Voter 346's Neighborhood 41°16'22"N 81°48'59"W approx. 3672, Lennox Circle, Brunswick, Medina County, Ohio, 44212, United States Precinct Margin: R+3%
Voter 347's Neighborhood 33°27'24"N 112°15'36"W approx. 9399, West Baden Street, Tolleson, Maricopa County, Arizona, 85353, United States Precinct Margin: D+52%	Voter 348's Neighborhood 42°49'45"N 88°8'50"W approx. 25875, West Loomis Road, Wind Lake, Town of Norway, Racine County, Wisconsin, 53185, United States Precinct Margin: R+48%
Voter 349's Neighborhood 37°57'31"N 122°3'6"W approx. Iron Horse Trail, Sherman Acres, Pleasant Hill, Contra Costa County, California, 1355, United States Precinct Margin: D+49%	Voter 350's Neighborhood 39°59'23"N 82°43'45"W approx. 6849, Mink Street Southwest, Wagram, Pataskala, Etna Township, Licking County, Ohio, 43062, United States Precinct Margin: R+8%
Voter 351's Neighborhood 31°17'18"N 81°20'59"W approx. 934, Champney, Glynn County, Georgia, 31522, United States Precinct Margin: R+36%	Voter 352's Neighborhood 37°37'14"N 120°19'32"W approx. Prouty Road, Mariposa County, California, United States Precinct Margin: R+34%
Voter 353's Neighborhood 37°51'0"N 121°58'31"W approx. 3257, Stone Valley Road, Contra Costa County, California, 94507, United States Precinct Margin: D+22%	Voter 354's Neighborhood 41°3'17"N 73°33'16"W approx. 32, Merrell Avenue, Stamford, Fairfield County, Connecticut, 06902, United States Precinct Margin: D+65%
Voter 355's Neighborhood 38°51'2"N 77°3'5"W approx. Capital Bikeshare, 26th Street South, National Landing, Crystal City, Arlington, Arlington County, Virginia, 22202, United States Precinct Margin: D+61%	Voter 356's Neighborhood 39°54'44"N 75°10'49"W approx. 1917, Schley Street, Packer Park, South Philadelphia, Philadelphia, Philadelphia County, Pennsylvania, 19145, United States Precinct Margin: R+44%
Voter 357's Neighborhood 39°5'6"N 94°36'5"W approx. 2325, Fairmount Avenue, West Side, Kansas City, Jackson County, Missouri, 64108, United States Precinct Margin: D+65%	Voter 358's Neighborhood 47°45'52"N 117°24'13"W approx. Pine Acres Par 3, East Regina Road, Fairwood, Spokane County, Washington, 99218-1929, United States Precinct Margin: R+19%
Voter 359's Neighborhood 46°50'51"N 92°6'21"W approx. Ridgeview Country Club, 700, West Redwing Street, Duluth, Saint Louis County, Minnesota, 55803, United States Precinct Margin: D+31%	Voter 360's Neighborhood 36°4'15"N 84°11'47"W approx. 191, Orchard Crest Circle, Anderson County, Tennessee, 37716, United States Precinct Margin: R+44%
Voter 361's Neighborhood 30°26'26"N 97°44'59"W approx. 6511, Melrose Trail, Milwood, Austin, Travis County, Texas, 78727, United States Precinct Margin: D+48%	Voter 362's Neighborhood 38°58'57"N 77°31'23"W approx. Bobolink Alley, Brambleton, Loudoun County, Virginia, 20107, United States Precinct Margin: D+32%
Voter 363's Neighborhood 40°45'46"N 111°34'38"W approx. 5192, Homestead Road, Jeremy Ranch, Summit County, Utah, 84098, United States Precinct Margin: D+17%	Voter 364's Neighborhood 43°5'3"N 77°27'10"W approx. 17, Clarkes Crossing, Village of Fairport, Town of Perinton, Monroe County, New York, 14450, United States Precinct Margin: D+22%
Voter 365's Neighborhood 41°57'21"N 70°40'5"W approx. 35, Russell Street, Plymouth, Plymouth County, Massachusetts, 02360, United States Precinct Margin: D+29%	Voter 366's Neighborhood 25°37'16"N 80°26'23"W approx. 15264, Southwest 156th Terrace, Miami-Dade County, Florida, 33187, United States Precinct Margin: R+3%
Voter 367's Neighborhood 34°0'17"N 118°16'7"W approx. 379, East 43rd Place, Historic South-Central, Los Angeles, Los Angeles County, California, 90011, United States Precinct Margin: D+72%	Voter 368's Neighborhood 47°19'11"N 122°24'39"W approx. Picnic Point Beach Trail, Federal Way, King County, Washington, United States Precinct Margin: D+23%
Voter 369's Neighborhood 33°9'17"N 117°17'47"W approx. 3414, Four Peaks Street, The Foothills, Calavera, Carlsbad, San Diego County, California, 92010, United States Precinct Margin: D+15%	Voter 370's Neighborhood 30°13'42"N 92°39'25"W approx. Song of Praise Church, 4th Street, Jennings, Jefferson Davis Parish, Louisiana, 70546, United States Precinct Margin: R+68%
Voter 371's Neighborhood 33°57'20"N 117°17'42"W approx. 21069, Penunuri Place, Moreno Valley, Riverside County, California, 92557, United States Precinct Margin: D+30%	Voter 372's Neighborhood 25°46'47"N 80°24'20"W approx. 12932, Northwest 10th Street, Miami-Dade County, Florida, 33182, United States Precinct Margin: R+24%
Voter 373's Neighborhood 26°1'18"N 80°14'42"W approx. 7845, Northwest 15th Street, Pembroke Pines, Broward County, Florida, 33024, United States Precinct Margin: D+7%	Voter 374's Neighborhood 35°22'11"N 118°56'15"W approx. 763, Crane Street, Kern County, California, 93306, United States Precinct Margin: D+31%
Voter 375's Neighborhood 42°43'30"N 71°27'56"W approx. 11, Warton Road, Ward 8, Nashua, Hillsborough County, New Hampshire, 03062, United States Precinct Margin: D+27%	Voter 376's Neighborhood 43°19'48"N 88°17'6"W approx. Slinger High School, Beine Street, Slinger, Washington County, Wisconsin, 53086, United States Precinct Margin: R+43%
Voter 377's Neighborhood 42°47'35"N 83°42'11"W approx. Millpond Manor, 201, East Elizabeth Street, Fenton, Genesee County, Michigan, 48430, United States Precinct Margin: R+9%	Voter 378's Neighborhood 41°27'18"N 88°0'14"W approx. 23822, Manhattan Road, Will County, Illinois, 60442, United States Precinct Margin: R+19%
Voter 379's Neighborhood 29°57'16"N 81°34'50"W approx. 8538, Beverly Lane, Saint Johns County, Florida, 32092, United States Precinct Margin: R+50%	Voter 380's Neighborhood 42°55'31"N 83°42'58"W approx. 7143, Brewer Road, Mundy Township, Genesee County, Michigan, 48507, United States Precinct Margin: D+5%
Voter 381's Neighborhood 32°14'2"N 110°53'56"W approx. 990, North Catalina Avenue, Tucson, Pima County, Arizona, 85711, United States Precinct Margin: D+49%	Voter 382's Neighborhood 36°55'45"N 76°14'5"W approx. 8424, Radnor Road, Brookfield Park, Norfolk, Virginia, 23503, United States Precinct Margin: D+1%
Voter 383's Neighborhood 40°38'47"N 74°11'40"W approx. 163, Butler Street, Liberty Square, Elizabeth, Union County, New Jersey, 07206, United States Precinct Margin: D+53%	Voter 384's Neighborhood 36°6'26"N 119°34'3"W approx. Letts Street, Corcoran, Kings County, California, 93212, United States Precinct Margin: D+19%
Voter 385's Neighborhood 33°56'53"N 84°54'27"W approx. 4575, Mc Pherson Church Road, Hanlin, Paulding County, Georgia, 30132, United States Precinct Margin: R+17%	Voter 386's Neighborhood 40°46'12"N 73°57'22"W approx. 310, East 75th Street, Manhattan Community Board 8, Lenox Hill, New York County, City of New York, New York, 10021, United States Precinct Margin: D+57%
Voter 387's Neighborhood 47°41'1"N 116°46'18"W approx. 1019, North 10th Street, Coeur d'Alene, Kootenai County, Idaho, 83814, United States Precinct Margin: D+6%	Voter 388's Neighborhood 34°6'14"N 117°51'55"W approx. 5036, Arroway Avenue, Covina, Los Angeles County, California, 91724, United States Precinct Margin: D+20%
Voter 389's Neighborhood 40°46'2"N 77°47'17"W approx. 610, South Academy Street, Boalsburg, Harris Township, Centre County, Pennsylvania, 16827, United States Precinct Margin: D+21%	Voter 390's Neighborhood 39°56'35"N 76°42'57"W approx. Irving Road, South Wood Hills, York, Spring Garden Township, York County, Pennsylvania, 17403, United States Precinct Margin: D+16%
Voter 391's Neighborhood 39°4'38"N 108°35'51"W approx. 473, Dike Road, Grand Junction, Mesa County, Colorado, 81507, United States Precinct Margin: R+6%	Voter 392's Neighborhood 42°7'6"N 88°15'0"W approx. 18, Sparrow Road, Carpentersville, Dundee Township, Kane County, Illinois, 60110, United States Precinct Margin: D+37%
Voter 393's Neighborhood 37°21'28"N 95°16'41"W approx. 2719, Pine Avenue, Orchard Park, Parsons, Labette County, Kansas, 67357, United States Precinct Margin: R+10%	Voter 394's Neighborhood 48°26'27"N 122°20'9"W approx. 330, Pacific Place, Mount Vernon, Skagit County, Washington, 98273, United States Precinct Margin: D+14%
Voter 395's Neighborhood 45°45'5"N 122°53'16"W approx. 33052, Southwest Keyes Road, Scappoose, Columbia County, Oregon, 97056, United States Precinct Margin: D+7%	Voter 396's Neighborhood 38°52'1"N 77°27'13"W approx. 5240, Glen Meadow Road, Centreville, Fairfax County, Virginia, 20120, United States Precinct Margin: D+31%
Voter 397's Neighborhood 30°0'19"N 91°49'16"W approx. 178, West Washington Street, Leesburg, New Iberia, Iberia Parish, Louisiana, 70560, United States Precinct Margin: D+56%	Voter 398's Neighborhood 31°10'50"N 94°22'5"W approx. 282, Dogwood Glen Street, Angelina County, Texas, 75980, United States Precinct Margin: R+81%
Voter 399's Neighborhood 33°58'9"N 83°22'40"W approx. 1005, College Avenue, Athens-Clarke County Unified Government, Athens-Clarke County, Georgia, 30601, United States Precinct Margin: D+61%	Voter 400's Neighborhood 28°29'48"N 82°32'1"W approx. 4399, Goldcoast Avenue, Spring Hill, Hernando County, Florida, 34609, United States Precinct Margin: R+18%
Voter 401's Neighborhood 41°32'24"N 74°6'40"W approx. 550, South Plank Road, Orange Lake, Village of Walden, Town of Newburgh, Orange County, New York, 12586, United States Precinct Margin: D+8%	Voter 402's Neighborhood 41°28'21"N 93°11'8"W approx. 340, 85th Avenue, Marion County, Iowa, 50170, United States Precinct Margin: R+44%
Voter 403's Neighborhood 41°44'30"N 87°35'6"W approx. 8401-8423, South Stony Island Avenue, Pierces Park, Avalon Park, Chicago, Hyde Park Township, Cook County, Illinois, 60617, United States Precinct Margin: D+91%	Voter 404's Neighborhood 32°32'58"N 85°7'36"W approx. 199, County Road 770, Lee County, Alabama, 36877, United States Precinct Margin: R+38%
Voter 405's Neighborhood 47°42'17"N 117°23'18"W approx. 1516, East Crown Avenue, Whitman, Hillyard, Spokane, Spokane County, Washington, 99207, United States Precinct Margin: D+2%	Voter 406's Neighborhood 29°21'34"N 98°25'27"W approx. 855, Utopia Lane, San Antonio, Bexar County, Texas, 78223, United States Precinct Margin: D+24%
Voter 407's Neighborhood 45°0'28"N 93°23'38"W approx. 2723, Ensign Circle, New Hope, Hennepin County, Minnesota, 55427, United States Precinct Margin: D+42%	Voter 408's Neighborhood 38°52'18"N 90°7'11"W approx. 699, Niagara Street, East Alton, Madison County, Illinois, 62024, United States Precinct Margin: R+23%
Voter 409's Neighborhood 38°51'30"N 77°12'27"W approx. 7609, Trail Run Road, West Falls Church, Fairfax County, Virginia, 22042, United States Precinct Margin: D+39%	Voter 410's Neighborhood 28°49'8"N 81°9'35"W approx. Yellow Trail, Volusia County, Florida, 32764, United States Precinct Margin: R+58%
Voter 411's Neighborhood 41°35'25"N 72°54'26"W approx. 18, Great Pine Path, Marion Historic District, Southington, Hartford County, Connecticut, 06479, United States Precinct Margin: R+4%	Voter 412's Neighborhood 39°9'27"N 91°23'5"W approx. 4898, County Road 424, Pike County, Missouri, 63359, United States Precinct Margin: R+68%
Voter 413's Neighborhood 45°6'18"N 93°20'59"W approx. 8345, Scott Avenue North, Brooklyn Park, Hennepin County, Minnesota, 55443, United States Precinct Margin: D+45%	Voter 414's Neighborhood 40°8'51"N 89°22'44"W approx. 399, South Adams Street, Lincoln, Logan County, Illinois, 62656, United States Precinct Margin: R+23%
Voter 415's Neighborhood 47°23'15"N 117°10'36"W approx. Zion Lutheran Church, West Hamilton Avenue, Fairfield, Spokane County, Washington, United States Precinct Margin: R+41%	Voter 416's Neighborhood 41°59'53"N 87°42'11"W approx. 6415-6425, North Richmond Street, West Ridge, Chicago, Rogers Park Township, Cook County, Illinois, 60645, United States Precinct Margin: D+8%
Voter 417's Neighborhood 29°22'57"N 95°3'21"W approx. Dump Road, La Marque, Galveston County, Texas, 77510, United States Precinct Margin: R+8%	Voter 418's Neighborhood 31°53'8"N 101°57'19"W approx. 10425, South County Road 1138, Midland County, Texas, 79706, United States Precinct Margin: R+71%
Voter 419's Neighborhood 33°9'54"N 97°8'23"W approx. 869, Sanders Road, Denton, Denton County, Texas, 76210, United States Precinct Margin: R+14%	Voter 420's Neighborhood 35°59'34"N 79°56'59"W approx. 665, West Main Street, Jamestown, Guilford County, North Carolina, 27282, United States Precinct Margin: R+3%
Voter 421's Neighborhood 33°57'19"N 118°7'21"W approx. 9730, Downey Avenue, Downey, Los Angeles County, California, 90240, United States Precinct Margin: D+26%	Voter 422's Neighborhood 29°34'12"N 98°30'3"W approx. 200, Bluff Hollow, San Antonio, Bexar County, Texas, 78216, United States Precinct Margin: D+2%
Voter 423's Neighborhood 33°47'5"N 118°8'49"W approx. 3873, East 14th Street, Long Beach, Los Angeles County, California, 90804, United States Precinct Margin: D+52%	Voter 424's Neighborhood 45°35'16"N 122°21'5"W approx. 1990, North Washougal River Road, Washougal, Clark County, Washington, 98671, United States Precinct Margin: R+1%
Voter 425's Neighborhood 41°49'29"N 72°40'30"W approx. 637, Matianuck Avenue, Windsor, Hartford County, Connecticut, 06095, United States Precinct Margin: D+74%	Voter 426's Neighborhood 33°30'30"N 111°55'29"W approx. FireSky Resort & Spa, East Chaparral Road, Scottsdale, Maricopa County, Arizona, 85251, United States Precinct Margin: D+17%
Voter 427's Neighborhood 36°18'15"N 115°16'37"W approx. Aurora Falls Street, Tule Springs, Las Vegas, Clark County, Nevada, 89159, United States Precinct Margin: R+16%	Voter 428's Neighborhood 29°7'12"N 82°18'7"W approx. Southwest 110th Avenue, York, Marion County, Florida, 34481, United States Precinct Margin: R+22%
Voter 429's Neighborhood 40°20'46"N 79°59'38"W approx. 5147, Curry Road, Baldwin, Allegheny County, Pennsylvania, 15236, United States Precinct Margin: D+3%	Voter 430's Neighborhood 40°51'50"N 107°48'55"W approx. County Road 102, Moffat County, Colorado, United States Precinct Margin: R+70%
Voter 431's Neighborhood 26°0'35"N 80°8'1"W approx. 1351, Van Buren Street, Hollywood, Broward County, Florida, 33019, United States Precinct Margin: D+23%	Voter 432's Neighborhood 39°16'20"N 81°31'59"W approx. 1942, 20th Street, North Parkersburg, Parkersburg, Wood County, West Virginia, 26101, United States Precinct Margin: R+31%
Voter 433's Neighborhood 35°4'42"N 89°53'4"W approx. 2671, Mount Moriah Road, Memphis, Shelby County, Tennessee, 38115, United States Precinct Margin: D+81%	Voter 434's Neighborhood 40°49'38"N 73°5'17"W approx. 21, Walter Street, Suffolk County, New York, 11741, United States Precinct Margin: R+24%
Voter 435's Neighborhood 42°55'19"N 84°40'14"W approx. 7494, Church Road, Riley, Riley Township, Clinton County, Michigan, 48879, United States Precinct Margin: R+27%	Voter 436's Neighborhood 30°22'24"N 94°20'59"W approx. 2526, FM 1293, Kountze, Hardin County, Texas, 77625, United States Precinct Margin: R+88%
Voter 437's Neighborhood 36°5'12"N 115°18'16"W approx. 9718, Maple Sugar Leaf Place, Spring Valley, Clark County, Nevada, 89148, United States Precinct Margin: D+21%	Voter 438's Neighborhood 37°24'49"N 76°33'50"W approx. Fiddlers Green Road, Gloucester County, Virginia, 23061, United States Precinct Margin: R+35%
Voter 439's Neighborhood 40°48'27"N 75°36'52"W approx. 291, Harvard Avenue, Palmerton, Carbon County, Pennsylvania, 18071, United States Precinct Margin: R+24%	Voter 440's Neighborhood 34°59'45"N 82°22'18"W approx. 337, Virginia Road, Travelers Rest, Greenville County, South Carolina, 29690, United States Precinct Margin: R+57%
Voter 441's Neighborhood 40°27'32"N 79°59'59"W approx. 1408, Howard Street, East Allegheny, Pittsburgh, Allegheny County, Pennsylvania, 15212, United States Precinct Margin: D+29%	Voter 442's Neighborhood 31°27'53"N 91°20'15"W approx. 12, McCalip-Retirement Pltn Road, Adams County, Mississippi, 39120, United States Precinct Margin: R+68%
Voter 443's Neighborhood 32°22'31"N 88°44'21"W approx. 5612, Semmes Road, Complete, Meridian, Lauderdale County, Mississippi, 39307, United States Precinct Margin: D+63%	Voter 444's Neighborhood 34°6'56"N 79°17'49"W approx. Olivet Cemetary Road, Marion County, South Carolina, 29589, United States Precinct Margin: D+34%
Voter 445's Neighborhood 41°52'31"N 73°34'4"W approx. 445, Cascade Mountain Road, Town of Amenia, Dutchess County, New York, 12501, United States Precinct Margin: D+2%	Voter 446's Neighborhood 33°19'57"N 87°6'17"W approx. 6128, Blue Creek Road, Valley Creek, Hueytown, Jefferson County, Alabama, 35444, United States Precinct Margin: R+32%
Voter 447's Neighborhood 37°28'6"N 122°14'17"W approx. 1118, Valota Road, Redwood City, San Mateo County, California, 94061, United States Precinct Margin: D+64%	Voter 448's Neighborhood 27°17'12"N 80°24'4"W approx. 1749, Southwest Commerce Avenue, Port Saint Lucie, Saint Lucie County, Florida, 34953, United States Precinct Margin: D+8%
Voter 449's Neighborhood 40°42'18"N 112°5'57"W approx. Cyprus High School, Spencer Avenue, Magna, Salt Lake County, Utah, 84044, United States Precinct Margin: D+5%	Voter 450's Neighborhood 38°58'45"N 86°32'44"W approx. 461, Cedar View Lane, Lawrence County, Indiana, 47421, United States Precinct Margin: R+52%
Voter 451's Neighborhood 41°41'5"N 86°17'6"W approx. 2489, Westmoor Street, South Bend, Saint Joseph County, Indiana, 46628, United States Precinct Margin: D+73%	Voter 452's Neighborhood 40°20'29"N 86°46'29"W approx. 6825, Wyandotte Road, Tippecanoe County, Indiana, 47905, United States Precinct Margin: R+44%
Voter 453's Neighborhood 35°2'29"N 107°31'26"W approx. Indian Service Route 24, Seama, Cibola County, New Mexico, 87007, United States Precinct Margin: D+66%	Voter 454's Neighborhood 26°49'40"N 80°5'23"W approx. 1853, Giralda Circle West, Palm Beach Gardens, North Palm Beach, Palm Beach County, Florida, 33410, United States Precinct Margin: R+5%
Voter 455's Neighborhood 43°42'19"N 114°20'16"W approx. Trail Creek Golf Course, Prospect Hill Loop, Sun Valley, Blaine County, Idaho, 83353, United States Precinct Margin: D+33%	Voter 456's Neighborhood 42°8'24"N 72°21'1"W approx. 152, Hovey Road, Monson, Hampden County, Massachusetts, 01069, United States Precinct Margin: R+5%
Voter 457's Neighborhood 41°30'43"N 88°9'9"W approx. Illinois Youth Correction Center, McDonough Street, Joliet, Will County, Illinois, 60435, United States Precinct Margin: D+44%	Voter 458's Neighborhood 42°33'27"N 83°47'33"W approx. Woodland Lake Motel, 8029, West Grand River Avenue, Brighton Township, Livingston County, Michigan, 48114, United States Precinct Margin: R+27%
Voter 459's Neighborhood 29°1'43"N 82°0'31"W approx. 9073, Southeast 130th Loop, Marion County, Florida, 34491, United States Precinct Margin: R+27%	Voter 460's Neighborhood 41°7'55"N 81°39'39"W approx. 199, Lethbridge Circle, Stoney Hill, Copley Township, Summit County, Ohio, 44321, United States Precinct Margin: D+15%
Voter 461's Neighborhood 40°7'9"N 75°7'55"W approx. 1081, Edge Hill Road, Mount Vernon Gardens, Abington, Abington Township, Montgomery County, Pennsylvania, 19001, United States Precinct Margin: D+42%	Voter 462's Neighborhood 36°37'27"N 94°28'36"W approx. 1781, Hobbs Road, McDonald County, Missouri, 64831, United States Precinct Margin: R+69%
Voter 463's Neighborhood 39°0'54"N 95°46'0"W approx. 6220, Southwest 29th Street, Topeka, Shawnee County, Kansas, 66614, United States Precinct Margin: D+40%	Voter 464's Neighborhood 43°34'59"N 124°5'8"W approx. 4000 Road, Coos County, Oregon, 97449, United States Precinct Margin: R+32%
Voter 465's Neighborhood 34°5'23"N 117°56'6"W approx. San Bernardino Road, West Covina, Los Angeles County, California, 91722, United States Precinct Margin: D+35%	Voter 466's Neighborhood 34°5'19"N 118°17'48"W approx. 954, North Kenmore Avenue, Bicycle District, East Hollywood, Los Angeles, Los Angeles County, California, 90029, United States Precinct Margin: D+53%
Voter 467's Neighborhood 40°54'42"N 73°54'2"W approx. 6154, Liebig Avenue, Bronx County, The Bronx, City of New York, New York, 10471, United States Precinct Margin: D+41%	Voter 468's Neighborhood 32°33'34"N 89°5'36"W approx. 333, Sessions Road, Newton County, Mississippi, 39365, United States Precinct Margin: R+76%
Voter 469's Neighborhood 32°39'51"N 97°28'17"W approx. Winscott Road, Benbrook, Tarrant County, Texas, 76126, United States Precinct Margin: R+28%	Voter 470's Neighborhood 34°4'45"N 118°7'53"W approx. The Church of Jesus Christ of Latter-day Saints, Shorb Street, Alhambra, Los Angeles County, California, 91801, United States Precinct Margin: D+39%
Voter 471's Neighborhood 36°55'24"N 76°15'47"W approx. 8059, West Glen Road, Denby Park, Monticello Village, Norfolk, Virginia, 23505, United States Precinct Margin: D+45%	Voter 472's Neighborhood 47°2'49"N 122°50'13"W approx. Dirty Dave's Pizza Parlor, Martin Way East, Olympia, Thurston County, Washington, 98506-5049, United States Precinct Margin: D+26%
Voter 473's Neighborhood 41°41'17"N 87°47'36"W approx. 11185, South Worth Avenue, Worth, Worth Township, Cook County, Illinois, 60482, United States Precinct Margin: R+7%	Voter 474's Neighborhood 43°11'17"N 112°20'20"W approx. 267, North Stout Avenue, Blackfoot, Bingham County, Idaho, 83221, United States Precinct Margin: R+58%
Voter 475's Neighborhood 33°55'57"N 118°0'35"W approx. 15199, Fernview Street, Los Angeles County, California, 90604, United States Precinct Margin: D+21%	Voter 476's Neighborhood 37°25'7"N 92°48'40"W approx. Letterman Cemetery, Bowen Creek Road, Webster County, Missouri, 65713, United States Precinct Margin: R+68%
Voter 477's Neighborhood 40°35'45"N 124°8'53"W approx. 1700, Stillman Way, Fortuna, Humboldt County, California, 95540, United States Precinct Margin: R+6%	Voter 478's Neighborhood 32°58'34"N 83°47'22"W approx. Klopfer Road, Bolingbroke, Monroe County, Georgia, 31004, United States Precinct Margin: R+56%
Voter 479's Neighborhood 30°12'33"N 97°48'5"W approx. 1911, Cannonwood Lane, Cherry Creek, Austin, Travis County, Texas, 78745, United States Precinct Margin: D+65%	Voter 480's Neighborhood 39°43'51"N 74°19'53"W approx. Micaja S Road, Stafford Township, Ocean County, New Jersey, 08050-2808, United States Precinct Margin: R+25%
Voter 481's Neighborhood 41°50'5"N 71°24'12"W approx. Hope High School, 324, Hope Street, College Hill, Providence, Providence County, Rhode Island, 02906, United States Precinct Margin: D+80%	Voter 482's Neighborhood 35°2'42"N 81°1'51"W approx. 2095, Driftwood Circle, York County, South Carolina, 29708, United States Precinct Margin: R+13%
Voter 483's Neighborhood 40°28'0"N 84°17'23"W approx. 7523, Botkins Road, Botkins, Shelby County, Ohio, 45306, United States Precinct Margin: R+76%	Voter 484's Neighborhood 39°3'51"N 119°45'33"W approx. Heybourne Road, Johnson Lane, Douglas County, Nevada, 89705, United States Precinct Margin: R+36%
Voter 485's Neighborhood 42°37'9"N 82°32'26"W approx. 927, Columbia Street, Pointe aux Chenes, Algonac, Saint Clair County, Michigan, 48001, United States Precinct Margin: R+37%	Voter 486's Neighborhood 40°42'27"N 80°17'6"W approx. 498, Ohio Avenue, Rochester, Beaver County, Pennsylvania, 15074, United States Precinct Margin: D+10%
Voter 487's Neighborhood 45°5'39"N 94°6'42"W approx. 10140, 40th Street Southwest, Middleville Township, Wright County, Minnesota, 55349, United States Precinct Margin: R+56%	Voter 488's Neighborhood 36°8'58"N 96°7'58"W approx. 129th West Avenue, Sand Springs, Tulsa County, Oklahoma, 74063, United States Precinct Margin: R+43%
Voter 489's Neighborhood 39°22'23"N 76°41'58"W approx. 3117, Northbrook Road, Wellwood, Pikesville, Baltimore County, Maryland, 21208, United States Precinct Margin: R+11%	Voter 490's Neighborhood 35°11'50"N 82°17'37"W approx. Hogback Mountain Road, Greenville County, South Carolina, United States Precinct Margin: D+5%
Voter 491's Neighborhood 33°12'15"N 96°57'0"W approx. 809, Lake Forest Trail, Denton County, Texas, 75068, United States Precinct Margin: D+13%	Voter 492's Neighborhood 32°44'41"N 97°13'35"W approx. 2329, Pollard Street, Fort Worth, Tarrant County, Texas, 76112, United States Precinct Margin: D+66%
Voter 493's Neighborhood 47°40'20"N 122°15'57"W approx. 6008, 57th Avenue Northeast, Windermere, Seattle, King County, Washington, 98115, United States Precinct Margin: D+83%	Voter 494's Neighborhood 43°31'38"N 116°5'4"W approx. BLM Track, Ada County, Idaho, 83715, United States Precinct Margin: D+12%
Voter 495's Neighborhood 34°13'9"N 81°32'24"W approx. Lovelace Family Medicine, P.A, 600, North Wheeler Ave, Prosperity, Newberry County, South Carolina, 29127, United States Precinct Margin: R+10%	Voter 496's Neighborhood 36°37'5"N 80°13'39"W approx. 440, New Hope Church Road, Patrick County, Virginia, 24171, United States Precinct Margin: R+56%
Voter 497's Neighborhood 33°38'56"N 112°3'46"W approx. Bona Venture Mobile Home Park, East Grovers Avenue, Quail Country Place, Phoenix, Maricopa County, Arizona, 85023-1501, United States Precinct Margin: D+2%	Voter 498's Neighborhood 45°47'28"N 122°33'18"W approx. 1702, Northwest 14th Circle, Battle Ground, Clark County, Washington, 98604, United States Precinct Margin: R+26%
Voter 499's Neighborhood 41°48'44"N 87°41'56"W approx. 4445, South Sacramento Avenue, Brighton Park, Chicago, Lake Township, Cook County, Illinois, 60632, United States Precinct Margin: D+64%	Voter 500's Neighborhood 40°30'9"N 78°25'3"W approx. 944, 28th Street, Westmont, Altoona, Blair County, Pennsylvania, 16601, United States Precinct Margin: R+22%
Voter 501's Neighborhood 34°9'29"N 118°22'29"W approx. 11210, La Maida Street, Los Angeles, Los Angeles County, California, 91601, United States Precinct Margin: D+76%	Voter 502's Neighborhood 47°56'29"N 122°14'58"W approx. Industry Street, Everett, Snohomish County, Washington, 98203, United States Precinct Margin: D+26%
Voter 503's Neighborhood 38°29'2"N 90°1'22"W approx. Mine Haul Road, Belleville, Saint Clair County, Illinois, 62220, United States Precinct Margin: R+14%	Voter 504's Neighborhood 46°41'32"N 95°52'5"W approx. 50342, Trowbridge Circle, Otter Tail County, Minnesota, 56587, United States Precinct Margin: R+45%
Voter 505's Neighborhood 29°42'48"N 95°47'52"W approx. 8753, Willowleaf Garden Crossing, Seven Meadows, Fort Bend County, Texas, 77494, United States Precinct Margin: R+7%	Voter 506's Neighborhood 32°36'32"N 80°19'35"W approx. 7793, Russell Creek Road, Charleston County, South Carolina, 29438, United States Precinct Margin: D+3%
Voter 507's Neighborhood 30°50'16"N 97°39'52"W approx. 235, Appaloosa Cove, Williamson County, Texas, 76527, United States Precinct Margin: R+31%	Voter 508's Neighborhood 39°42'8"N 91°22'51"W approx. 2311, Chestnut Street, Hannibal, Marion County, Missouri, 63401, United States Precinct Margin: R+19%
Voter 509's Neighborhood 36°21'59"N 76°40'41"W approx. 436, Perkins Road, Carter, Gates County, North Carolina, 27938, United States Precinct Margin: R+34%	Voter 510's Neighborhood 41°47'3"N 88°2'57"W approx. 5605, Katrine Avenue, Woodridge, DuPage County, Illinois, 60516, United States Precinct Margin: D+32%
Voter 511's Neighborhood 40°15'42"N 77°13'59"W approx. 1770, Longs Gap Road, Cumberland County, Pennsylvania, 17013, United States Precinct Margin: R+19%	Voter 512's Neighborhood 33°24'28"N 97°8'46"W approx. 3989, Huling Road, Denton County, Texas, 76266, United States Precinct Margin: R+58%
Voter 513's Neighborhood 33°13'8"N 93°15'38"W approx. 414, Columbia Rd 5, Horsehead, Columbia County, Arkansas, 71753, United States Precinct Margin: R+27%	Voter 514's Neighborhood 33°53'7"N 118°7'10"W approx. 16330, Cornuta Avenue, Bellflower, Los Angeles County, California, 90706, United States Precinct Margin: D+31%
Voter 515's Neighborhood 41°35'58"N 70°56'38"W approx. 32, Atlantic Street, Redgate Corner, Dartmouth, Bristol County, Massachusetts, 02748, United States Precinct Margin: D+27%	Voter 516's Neighborhood 33°35'54"N 83°51'30"W approx. 1157, Elm Street Northeast, Covington, Newton County, Georgia, 30014, United States Precinct Margin: R+1%
Voter 517's Neighborhood 33°41'38"N 88°45'26"W approx. Siloam-Una Road, Clay County, Mississippi, United States Precinct Margin: D+53%	Voter 518's Neighborhood 34°24'46"N 118°32'27"W approx. The Original Saugus Cafe, 25861, Railroad Avenue, Pardee, Santa Clarita, Los Angeles County, California, 91355, United States Precinct Margin: D+1%
Voter 519's Neighborhood 34°10'34"N 79°53'44"W approx. 1098, Whitehall Shores Road, Heritage, Florence County, South Carolina, 29501, United States Precinct Margin: R+9%	Voter 520's Neighborhood 40°25'49"N 111°50'49"W approx. Townhomes, East Crosscourt Way, Lehi, Utah County, Utah, United States Precinct Margin: R+56%
Voter 521's Neighborhood 33°43'13"N 118°2'47"W approx. 16642, Blanton Street, Huntington Beach, Orange County, California, 92649, United States Precinct Margin: D+8%	Voter 522's Neighborhood 42°38'8"N 74°20'21"W approx. 180, Riverview Road, Town of Middleburgh, Schoharie County, New York, 12157, United States Precinct Margin: R+42%
Voter 523's Neighborhood 45°24'0"N 122°47'17"W approx. 16565, Southwest 108th Avenue, Cook Park, Tigard, Washington County, Oregon, 97224, United States Precinct Margin: D+36%	Voter 524's Neighborhood 38°32'24"N 94°33'50"W approx. 32439, Nelson Road, Cass County, Missouri, 64742, United States Precinct Margin: R+56%
Voter 525's Neighborhood 27°41'39"N 97°24'38"W approx. 4130, Walnut Hills Drive, Corpus Christi, Nueces County, Texas, 78413, United States Precinct Margin: D+4%	Voter 526's Neighborhood 38°17'31"N 78°16'29"W approx. 77, Bethel Lane, Rochelle, Madison County, Virginia, 22738, United States Precinct Margin: R+30%
Voter 527's Neighborhood 41°16'41"N 73°55'58"W approx. Louisa Street, City of Peekskill, Westchester County, New York, 10566, United States Precinct Margin: D+36%	Voter 528's Neighborhood 41°41'28"N 86°52'6"W approx. 1722, Welnetz Road, Michigan City, LaPorte County, Indiana, 46360, United States Precinct Margin: D+48%
Voter 529's Neighborhood 40°41'8"N 73°58'15"W approx. Brooklyn Bear's Community Gardens - Carlton, Carlton Avenue, Brooklyn, Kings County, City of New York, New York, 11238, United States Precinct Margin: D+95%	Voter 530's Neighborhood 35°22'6"N 81°23'6"W approx. 408, West Old Post Road, Cherryville, Gaston County, North Carolina, 28021, United States Precinct Margin: R+47%
Voter 531's Neighborhood 43°57'24"N 91°0'37"W approx. Balmer Road, Town of Burns, La Crosse County, Wisconsin, United States Precinct Margin: R+22%	Voter 532's Neighborhood 37°41'36"N 77°37'39"W approx. 5739, Pouncey Tract Road, Henrico County, Virginia, 23059, United States Precinct Margin: R+2%
Voter 533's Neighborhood 42°10'12"N 87°49'2"W approx. 1598, Grove Avenue, Briergate, Highland Park, Lake County, Illinois, 60035, United States Precinct Margin: D+61%	Voter 534's Neighborhood 33°4'25"N 96°53'19"W approx. Tommy Briggs Cougar Stadium, Cougar Alley, The Colony, Denton County, Texas, 75056, United States Precinct Margin: D+4%
Voter 535's Neighborhood 41°41'33"N 111°50'3"W approx. Main Street, Millville, Cache County, Utah, 84326, United States Precinct Margin: R+58%	Voter 536's Neighborhood 34°43'25"N 84°44'6"W approx. Estelle Mddleton Road, Murray County, Georgia, United States Precinct Margin: R+77%
Voter 537's Neighborhood 33°44'25"N 117°25'36"W approx. 13375, Temescal Canyon Road, Alberhill, Lake Elsinore, Riverside County, California, 92883, United States Precinct Margin: R+4%	Voter 538's Neighborhood 41°44'48"N 87°46'4"W approx. 5882, 80th Street, Burbank, Stickney Township, Cook County, Illinois, 60459, United States Precinct Margin: D+4%
Voter 539's Neighborhood 34°6'43"N 84°27'44"W approx. 1606, Barnes Road, Woodstock, Cherokee County, Georgia, 30188, United States Precinct Margin: R+23%	Voter 540's Neighborhood 45°37'43"N 122°34'4"W approx. 10392, Northeast 10th Street, Marrion, Vancouver, Clark County, Washington, 98664, United States Precinct Margin: D+14%
Voter 541's Neighborhood 42°39'27"N 83°25'26"W approx. Suburban Ford of Waterford, 6975, Highland Road, Waterford Township, Oakland County, Michigan, 48327, United States Precinct Margin: D+4%	Voter 542's Neighborhood 35°7'53"N 81°5'54"W approx. 5898, Hidden Oaks Lane, York County, South Carolina, 29710, United States Precinct Margin: R+30%
Voter 543's Neighborhood 25°53'45"N 80°11'50"W approx. 90, Northeast 132nd Street, North Miami, Miami-Dade County, Florida, 33161, United States Precinct Margin: D+75%	Voter 544's Neighborhood 42°29'9"N 90°40'5"W approx. 201, River Ridge Street, South End District, Dubuque, Dubuque County, Iowa, 52003, United States Precinct Margin: D+18%
Voter 545's Neighborhood 37°58'33"N 122°29'9"W approx. 47, Lochinvar Road, San Rafael, Marin County, California, 94901, United States Precinct Margin: D+56%	Voter 546's Neighborhood 30°24'27"N 93°28'39"W approx. Tank Road, Calcasieu Parish, Louisiana, 70633, United States Precinct Margin: R+67%
Voter 547's Neighborhood 42°18'22"N 71°19'29"W approx. Crosstown Trail and Cochituate Aqueduct Trail, Overbrook, Wellesley, Norfolk County, Massachusetts, 01500, United States Precinct Margin: D+60%	Voter 548's Neighborhood 42°51'40"N 96°2'10"W approx. 13652, Pioneer Avenue, Plymouth County, Iowa, 51031, United States Precinct Margin: R+61%
Voter 549's Neighborhood 39°44'45"N 75°19'50"W approx. 115, Delaware Crossing, Woolwich Township, Gloucester County, New Jersey, 08085, United States Precinct Margin: D+3%	Voter 550's Neighborhood 29°39'5"N 95°33'20"W approx. 11696, Dover Street, Houston, Harris County, Texas, 77031, United States Precinct Margin: D+33%
Voter 551's Neighborhood 44°58'14"N 93°15'2"W approx. Brian Coyle Center, 420, 15th Avenue South, Phillips, Minneapolis, Hennepin County, Minnesota, 55454, United States Precinct Margin: D+84%	Voter 552's Neighborhood 36°47'49"N 76°7'23"W approx. Parkway Elementary, Macarthur Road, Salem, Virginia Beach, Virginia, 23456, United States Precinct Margin: D+43%
Voter 553's Neighborhood 38°44'48"N 121°11'39"W approx. 5748, Macargo Road, Placer County, California, 95746, United States Precinct Margin: R+9%	Voter 554's Neighborhood 40°31'41"N 86°51'57"W approx. 2191, Mert Lane, Tippecanoe County, Indiana, 47920, United States Precinct Margin: R+26%
Voter 555's Neighborhood 36°0'22"N 83°52'19"W approx. 129, Pelham Road, Chilhowee Hills, Knoxville, Knox County, Tennessee, 37914, United States Precinct Margin: D+65%	Voter 556's Neighborhood 34°11'49"N 118°37'11"W approx. 22629, Marlin Place, Los Angeles, Los Angeles County, California, 91307, United States Precinct Margin: D+29%
Voter 557's Neighborhood 40°35'24"N 112°0'52"W approx. 8757, Grizzly Way, West Jordan, Salt Lake County, Utah, 84081, United States Precinct Margin: R+32%	Voter 558's Neighborhood 35°48'11"N 80°50'20"W approx. 624, Old Farm Road, Old Farm, Statesville, Iredell County, North Carolina, 28625, United States Precinct Margin: R+17%
Voter 559's Neighborhood 42°15'38"N 75°32'44"W approx. 152, Morgan Hill Road, North Afton, Town of Afton, Chenango County, New York, 13730, United States Precinct Margin: R+33%	Voter 560's Neighborhood 30°24'40"N 95°32'52"W approx. 12305, Maggie Lane, Montgomery County, Texas, 77318, United States Precinct Margin: R+68%
Voter 561's Neighborhood 41°50'7"N 87°47'56"W approx. 3129, Wenonah Avenue, Berwyn, Cook County, Illinois, 60402, United States Precinct Margin: D+54%	Voter 562's Neighborhood 41°36'53"N 70°51'18"W approx. 6, Widemarsh Beach Way, Wigwam Beach, Fairhaven, Bristol County, Massachusetts, 02719, United States Precinct Margin: D+2%
Voter 563's Neighborhood 26°17'9"N 81°44'50"W approx. 6013, Manchester Place, Carlton Lakes, Collier County, Florida, 34110, United States Precinct Margin: R+24%	Voter 564's Neighborhood 43°38'46"N 116°19'34"W approx. 4500, North Tumbleweed Lane, Boise, Ada County, Idaho, 83713, United States Precinct Margin: R+12%
Voter 565's Neighborhood 37°57'12"N 86°42'47"W approx. 5087, Sky Blue Lane, Perry County, Indiana, 47520, United States Precinct Margin: R+30%	Voter 566's Neighborhood 40°50'43"N 72°48'13"W approx. Patricia Lane, Manor Woods, Suffolk County, New York, 11949, United States Precinct Margin: R+31%
Voter 567's Neighborhood 40°46'44"N 73°56'49"W approx. 402, East 90th Street, Manhattan Community Board 8, Yorkville, New York County, City of New York, New York, 10128, United States Precinct Margin: D+71%	Voter 568's Neighborhood 26°1'41"N 80°16'26"W approx. 2151, Northwest 96th Terrace, Pembroke Pines, Broward County, Florida, 33024, United States Precinct Margin: D+25%
Voter 569's Neighborhood 40°47'57"N 74°13'24"W approx. 47, Cedar Avenue, Montclair, Essex County, New Jersey, 07042, United States Precinct Margin: D+85%	Voter 570's Neighborhood 41°5'18"N 111°56'26"W approx. East Primrose Lane, Hidden Hollow, Layton, Davis County, Utah, 84040, United States Precinct Margin: R+20%
Voter 571's Neighborhood 30°36'53"N 98°28'39"W approx. Packsaddle Mountain Road, Llano County, Texas, 78639, United States Precinct Margin: R+51%	Voter 572's Neighborhood 38°52'2"N 77°8'39"W approx. Arlington Boulevard Service Road, Seven Corners, Fairfax County, Virginia, 22044, United States Precinct Margin: D+48%
Voter 573's Neighborhood 26°32'37"N 80°10'15"W approx. 7899, Rockford Road, Palm Beach County, Florida, 33472, United States Precinct Margin: D+33%	Voter 574's Neighborhood 35°48'26"N 81°18'6"W approx. 365, Chigger Ridge Road, Alexander County, North Carolina, 28681, United States Precinct Margin: R+57%
Voter 575's Neighborhood 33°30'30"N 111°55'29"W approx. FireSky Resort & Spa, East Chaparral Road, Scottsdale, Maricopa County, Arizona, 85251, United States Precinct Margin: D+17%	Voter 576's Neighborhood 32°44'30"N 93°45'36"W approx. Cedar Farm Lane, Bossier Parish, Louisiana, 71064, United States Precinct Margin: R+63%
Voter 577's Neighborhood 39°56'25"N 76°37'48"W approx. 641, Kendale Road, Freysville, Windsor Township, York County, Pennsylvania, 17356, United States Precinct Margin: R+29%	Voter 578's Neighborhood 43°39'18"N 93°21'59"W approx. 303, Johnson Street, Albert Lea, Freeborn County, Minnesota, 56007, United States Precinct Margin: R+8%
Voter 579's Neighborhood 41°6'18"N 73°33'18"W approx. 10, Hampshire Lane, Turn of River, Stamford, Fairfield County, Connecticut, 06905, United States Precinct Margin: D+21%	Voter 580's Neighborhood 37°6'47"N 77°36'7"W approx. 17415, Chamberlands Road, Dinwiddie County, Virginia, 23841, United States Precinct Margin: R+33%
Voter 581's Neighborhood 47°53'45"N 122°15'6"W approx. Arco, Evergreen Way, Fairmont, Holly, Everett, Snohomish County, Washington, 98204, United States Precinct Margin: D+33%	Voter 582's Neighborhood 35°19'33"N 80°58'39"W approx. 1469, Hart Road, Shuffletown, Charlotte, Mecklenburg County, North Carolina, 28214, United States Precinct Margin: D+37%
Voter 583's Neighborhood 32°41'51"N 97°39'17"W approx. 1819, Old Annetta Road, Annetta, Parker County, Texas, 76008, United States Precinct Margin: R+57%	Voter 584's Neighborhood 41°44'16"N 86°5'54"W approx. 11829, Buttercup Circle, Granger, Saint Joseph County, Indiana, 46530, United States Precinct Margin: R+19%
Voter 585's Neighborhood 34°12'54"N 118°26'10"W approx. 7944, Clearfield Avenue, Panorama City, Los Angeles, Los Angeles County, California, 91402, United States Precinct Margin: D+43%	Voter 586's Neighborhood 33°12'10"N 97°9'32"W approx. Athletic Center (ATHC), South Bonnie Brae Street, Denton, Denton County, Texas, 76203, United States Precinct Margin: D+28%
Voter 587's Neighborhood 37°58'16"N 122°17'42"W approx. 4501, Santa Rita Road, Richmond, Contra Costa County, California, 94803, United States Precinct Margin: D+69%	Voter 588's Neighborhood 44°38'58"N 93°14'1"W approx. 20708, Hartford Way, Village Creek, Lakeville, Dakota County, Minnesota, 55044, United States Precinct Margin: R+4%
Voter 589's Neighborhood 26°18'4"N 98°0'24"W approx. 955, Live Oak Street, Elsa, Hidalgo County, Texas, 78543, United States Precinct Margin: D+38%	Voter 590's Neighborhood 38°52'56"N 87°14'5"W approx. Begeman Cemetery, East Wagner Road, Knox County, Indiana, 47596, United States Precinct Margin: R+60%
Voter 591's Neighborhood 28°36'5"N 81°10'2"W approx. 4033, Shawn Circle, Tanner Crossings, Orange County, Florida, 32826, United States Precinct Margin: D+28%	Voter 592's Neighborhood 37°42'51"N 121°56'53"W approx. 11554, Vista Place, West Dublin, Dublin, Alameda County, California, 94583, United States Precinct Margin: D+35%
Voter 593's Neighborhood 35°11'37"N 80°42'50"W approx. 5116, Birchbark Lane, Silverstone, Charlotte, Mecklenburg County, North Carolina, 28227, United States Precinct Margin: D+43%	Voter 594's Neighborhood 34°10'15"N 117°18'51"W approx. 1399, Jeffrey Way, San Bernardino, San Bernardino County, California, 92407, United States Precinct Margin: D+28%
Voter 595's Neighborhood 30°31'2"N 97°44'33"W approx. Oak Brook Trail, Avery Ranch, Brushy Creek, Williamson County, Texas, 78781, United States Precinct Margin: D+17%	Voter 596's Neighborhood 48°12'4"N 96°46'11"W approx. 683, North 4th Street, Warren, Marshall County, Minnesota, 56762, United States Precinct Margin: R+49%
Voter 597's Neighborhood 39°22'14"N 84°23'49"W approx. Hamilton Mason Road, Liberty Township, Butler County, Ohio, 45069, United States Precinct Margin: R+8%	Voter 598's Neighborhood 36°7'47"N 115°17'45"W approx. 9125, West Desert Inn Road, Las Vegas, Clark County, Nevada, 89117, United States Precinct Margin: D+15%
Voter 599's Neighborhood 40°42'37"N 73°44'35"W approx. 106-19, 215th Street, Queens, City of New York, New York, 11429, United States Precinct Margin: D+88%	Voter 600's Neighborhood 39°10'42"N 75°59'10"W approx. 545, Ewingtown Road, Queen Anne's County, Maryland, 21623, United States Precinct Margin: R+26%
Voter 601's Neighborhood 33°48'58"N 117°55'51"W approx. Goodhue Avenue, Anaheim, Orange County, California, 92802, United States Precinct Margin: D+29%	Voter 602's Neighborhood 36°0'47"N 95°54'53"W approx. 10321, South Granite Avenue, Forest Pointe, Tulsa, Tulsa County, Oklahoma, 74137, United States Precinct Margin: R+44%
Voter 603's Neighborhood 34°1'39"N 118°6'51"W approx. 865, Marconi Street, Montebello, Los Angeles County, California, 90640, United States Precinct Margin: D+34%	Voter 604's Neighborhood 44°11'14"N 121°22'19"W approx. Mariposa lane, Deschutes County, Oregon, United States Precinct Margin: R+18%
Voter 605's Neighborhood 36°4'48"N 94°11'47"W approx. 1239, North West End Avenue, Fayetteville, Washington County, Arkansas, 72703, United States Precinct Margin: D+44%	Voter 606's Neighborhood 36°57'45"N 93°44'26"W approx. 1036, Autumn Lane, Aurora, Lawrence County, Missouri, 65605, United States Precinct Margin: R+60%
Voter 607's Neighborhood 32°59'5"N 97°22'30"W approx. 809, Mexicali Way, Fort Worth, Tarrant County, Texas, 76052, United States Precinct Margin: R+26%	Voter 608's Neighborhood 25°51'14"N 80°8'18"W approx. 7300, Trouville Esplanade, Isle of Normandy, Miami Beach, Miami-Dade County, Florida, 33141, United States Precinct Margin: D+34%
Voter 609's Neighborhood 36°2'28"N 95°52'22"W approx. Meadowbrook Country Club, 9300, East 81st Street, Highland Park, Tulsa, Tulsa County, Oklahoma, 74014, United States Precinct Margin: R+21%	Voter 610's Neighborhood 29°35'12"N 98°29'31"W approx. 241, Limestone Creek, Hill Country Village, Bexar County, Texas, 78232, United States Precinct Margin: R+34%
Voter 611's Neighborhood 42°15'6"N 83°26'29"W approx. I-275 Metro Trail, Van Buren Township, Wayne County, Michigan, 48111-1133, United States Precinct Margin: D+17%	Voter 612's Neighborhood 25°38'3"N 80°19'56"W approx. 8520, Southwest 146th Street, Rockdale, Palmetto Bay, Miami-Dade County, Florida, 33158, United States Precinct Margin: D+13%
Voter 613's Neighborhood 39°41'14"N 105°4'26"W approx. 6945, West Calahan Avenue, Lakewood, Jefferson County, Colorado, 80232, United States Precinct Margin: D+20%	Voter 614's Neighborhood 28°8'38"N 82°30'52"W approx. 4126, Highland Park Circle, Cheval, Hillsborough County, Florida, 33558, United States Precinct Margin: R+9%
Voter 615's Neighborhood 38°46'52"N 89°54'21"W approx. 7715, Goshen Road, Edwardsville, Madison County, Illinois, 62025, United States Precinct Margin: R+29%	Voter 616's Neighborhood 35°18'27"N 97°18'58"W approx. 16198, A Street, Cleveland County, Oklahoma, 73165, United States Precinct Margin: R+50%
Voter 617's Neighborhood 32°37'34"N 97°23'38"W approx. 4616, Bellflower Way, Fort Worth, Tarrant County, Texas, 76123, United States Precinct Margin: D+16%	Voter 618's Neighborhood 38°59'59"N 121°30'24"W approx. 2911, Leach Road, Yuba County, California, 95961, United States Precinct Margin: R+56%
Voter 619's Neighborhood 38°38'15"N 76°53'37"W approx. Salvation Army, Old Washington Road, Mattawoman, Waldorf, Charles County, Maryland, 20601, United States Precinct Margin: D+59%	Voter 620's Neighborhood 40°34'7"N 74°23'18"W approx. 30, Westwood Circle, New Petrograd, Edison, Middlesex County, New Jersey, 08820, United States Precinct Margin: D+24%
Voter 621's Neighborhood 37°40'21"N 121°47'52"W approx. 341, Jillana Avenue, Livermore, Alameda County, California, 94550, United States Precinct Margin: D+27%	Voter 622's Neighborhood 41°37'28"N 72°54'57"W approx. E Grannis Pond Road, Southington, Hartford County, Connecticut, 06010-7403, United States Precinct Margin: R+13%
Voter 623's Neighborhood 30°5'20"N 81°35'59"W approx. 499, Chattan Way, Fruit Cove, Saint Johns County, Florida, 32259, United States Precinct Margin: R+34%	Voter 624's Neighborhood 39°25'52"N 118°45'29"W approx. 1297, Lazy Heart Lane, Churchill County, Nevada, 89406, United States Precinct Margin: R+68%
Voter 625's Neighborhood 31°27'40"N 110°17'39"W approx. 489, East Ramsey Canyon Road, Bledsoe, Sierra Vista, Cochise County, Arizona, 85615, United States Precinct Margin: R+35%	Voter 626's Neighborhood 32°33'32"N 94°40'58"W approx. 685, Hickory Creek Lane, Harrison County, Texas, 75605, United States Precinct Margin: R+75%
Voter 627's Neighborhood 40°31'50"N 74°16'24"W approx. 913, Amboy Avenue, William Dunlap Homes, Perth Amboy, Woodbridge, Middlesex County, New Jersey, 08861, United States Precinct Margin: D+44%	Voter 628's Neighborhood 29°35'50"N 98°26'15"W approx. 17115, Redland Road, San Antonio, Bexar County, Texas, 78247, United States Precinct Margin: R+4%
Voter 629's Neighborhood 32°41'50"N 96°49'58"W approx. 542, Early Dawn Trail, Dallas, Dallas County, Texas, 75224, United States Precinct Margin: D+49%	Voter 630's Neighborhood 30°18'38"N 84°14'55"W approx. 9458, Old Woodville Road, Lutterloh, Woodville, Leon County, Florida, 32305, United States Precinct Margin: R+5%
Voter 631's Neighborhood 42°55'33"N 88°2'24"W approx. 6551, Parkedge Circle, Franklin, Milwaukee County, Wisconsin, 53132, United States Precinct Margin: R+1%	Voter 632's Neighborhood 42°24'2"N 88°10'29"W approx. 69, Cora Road, Fox Lake, Lake County, Illinois, 60020, United States Precinct Margin: R+7%
Voter 633's Neighborhood 32°39'51"N 94°16'0"W approx. Buckhorn Road, Harrison County, Texas, United States Precinct Margin: R+60%	Voter 634's Neighborhood 44°37'21"N 123°4'28"W approx. 2502, 20th Avenue Southeast, Albany, Linn County, Oregon, 97322, United States Precinct Margin: D+2%
Voter 635's Neighborhood 41°45'5"N 87°37'33"W approx. South Lafayette Avenue, Greater Grand Crossing, Chicago, Lake Township, Cook County, Illinois, 60621, United States Precinct Margin: D+96%	Voter 636's Neighborhood 39°9'3"N 84°4'48"W approx. 5698, Freedom Trail, Jackson Township, Clermont County, Ohio, 45103, United States Precinct Margin: R+69%
Voter 637's Neighborhood 46°57'27"N 123°46'26"W approx. 170, H Street, Cosmopolis, Grays Harbor County, Washington, 98537, United States Precinct Margin: R+7%	Voter 638's Neighborhood 36°25'6"N 79°6'5"W approx. John Brewer Road, Person County, North Carolina, 27291, United States Precinct Margin: R+47%
Voter 639's Neighborhood 39°9'34"N 76°39'40"W approx. BWI Trail, Glenbrook, Glen Burnie, Anne Arundel County, Maryland, 21144-1320, United States Precinct Margin: D+13%	Voter 640's Neighborhood 34°6'41"N 117°11'4"W approx. Beattie Middle School, Boulder Avenue, Highland, San Bernardino County, California, 92346-9998, United States Precinct Margin: D+9%
Voter 641's Neighborhood 41°41'17"N 81°16'7"W approx. 10325, Johnnycake Ridge Road, Lake County, Ohio, 44077, United States Precinct Margin: R+25%	Voter 642's Neighborhood 36°0'18"N 114°56'16"W approx. 1268, Dalene Avenue, River Mountain View Estates, Henderson, Clark County, Nevada, 89002, United States Precinct Margin: R+28%
Voter 643's Neighborhood 39°33'48"N 105°6'9"W approx. Falcon Bluffs Middle School, West Remington Place, Jefferson County, Colorado, 80127-5008, United States Precinct Margin: D+5%	Voter 644's Neighborhood 39°53'4"N 75°31'8"W approx. 809, Concord Road, Concordville, Concord Township, Delaware County, Pennsylvania, 19342, United States Precinct Margin: D+9%
Voter 645's Neighborhood 26°8'26"N 81°46'32"W approx. 1378, Embassy Lane, Collier County, Florida, 34104, United States Precinct Margin: R+21%	Voter 646's Neighborhood 33°42'21"N 118°0'59"W approx. 17641, Collins Circle, Huntington Beach, Orange County, California, 92647, United States Precinct Margin: R+8%
Voter 647's Neighborhood 32°33'50"N 117°3'0"W approx. Smythe Elementary School, 1880, Smythe Avenue, San Ysidro, San Diego, San Diego County, California, 92173, United States Precinct Margin: D+51%	Voter 648's Neighborhood 32°28'5"N 86°32'2"W approx. 551, Golson Road, Prattville, Autauga County, Alabama, 36067, United States Precinct Margin: R+38%
Voter 649's Neighborhood 41°28'0"N 96°47'9"W approx. Birchwood Manor, 1120, Walnut Street, North Bend, Dodge County, Nebraska, 68649, United States Precinct Margin: R+45%	Voter 650's Neighborhood 39°6'46"N 79°59'36"W approx. 63, Bear Run Road, Philippi, Barbour County, West Virginia, 26416, United States Precinct Margin: R+57%
Voter 651's Neighborhood 41°52'5"N 88°6'29"W approx. 201, West Union Avenue, Wheaton, DuPage County, Illinois, 60187, United States Precinct Margin: D+27%	Voter 652's Neighborhood 36°0'41"N 115°13'4"W approx. Aldeane Comito Ries Elementary School, West Le Baron Avenue, Enterprise, Clark County, Nevada, 89141, United States Precinct Margin: D+10%
Voter 653's Neighborhood 29°10'21"N 81°4'9"W approx. Volusia County Parks, Recreation & Cultural Maintenance / Tradeworkers, Bellevue Avenue, Daytona Beach, Volusia County, Florida, 32124, United States Precinct Margin: R+20%	Voter 654's Neighborhood 42°9'19"N 72°28'20"W approx. Healthsouth Rehabilitation Hospital Of Western Massachusetts, 222, State Street, Ludlow, Hampden County, Massachusetts, 01056, United States Precinct Margin: D+2%
Voter 655's Neighborhood 36°51'59"N 119°46'11"W approx. 722, East Shepherd Avenue, Fresno, Fresno County, California, 93720, United States Precinct Margin: D+1%	Voter 656's Neighborhood 45°34'3"N 68°13'12"W approx. 1032, Kingman Road, Kingman Township, Penobscot County, Maine, 04451, United States Precinct Margin: R+76%
Voter 657's Neighborhood 47°33'33"N 122°22'10"W approx. West Seattle Golf Course, Southwest Avalon Way, West Seattle, Seattle, King County, Washington, 98126, United States Precinct Margin: D+81%	Voter 658's Neighborhood 44°25'32"N 69°26'16"W approx. 1180, North Palermo Road, Carrs Corner, Palermo, Waldo County, Maine, 04354, United States Precinct Margin: R+16%
Voter 659's Neighborhood 41°2'22"N 81°25'39"W approx. Ripley Avenue, Springfield Township, Summit County, Ohio, 44312, United States Precinct Margin: R+30%	Voter 660's Neighborhood 40°38'34"N 111°50'49"W approx. 6099, East Village Road, Murray, Salt Lake County, Utah, 84121, United States Precinct Margin: D+16%
Voter 661's Neighborhood 40°49'56"N 74°9'40"W approx. 60, Oakley Terrace, Nutley, Essex County, New Jersey, 07110, United States Precinct Margin: D+3%	Voter 662's Neighborhood 42°49'31"N 71°18'43"W approx. 49, Londonderry Road, Windham, Rockingham County, New Hampshire, 03087, United States Precinct Margin: R+6%
Voter 663's Neighborhood 45°13'25"N 71°19'20"W approx. Indian Stream Road, Pittsburg, Coos County, New Hampshire, United States Precinct Margin: R+41%	Voter 664's Neighborhood 42°15'20"N 84°25'36"W approx. 707, Eaton Street, Jackson, Jackson County, Michigan, 49202, United States Precinct Margin: D+7%
Voter 665's Neighborhood 36°5'40"N 80°9'58"W approx. 487, Quail Haven Lane, Woodbridge, Winston-Salem, Forsyth County, North Carolina, 27107, United States Precinct Margin: D+24%	Voter 666's Neighborhood 42°35'33"N 71°7'11"W approx. 5, Voke Street, North Reading, Middlesex County, Massachusetts, 01864-1298, United States Precinct Margin: D+19%
Voter 667's Neighborhood 39°53'36"N 75°19'44"W approx. 512, 6th Avenue, Folsom, Ridley Township, Delaware County, Pennsylvania, 19033, United States Precinct Margin: R+7%	Voter 668's Neighborhood 33°27'0"N 94°25'1"W approx. 3, Park Place, Boston, New Boston, Bowie County, Texas, 75570, United States Precinct Margin: R+65%
Voter 669's Neighborhood 33°52'16"N 84°32'4"W approx. Smyrna Fire Station #2, 642, Concord Road Southeast, Smyrna, Cobb County, Georgia, 30080, United States Precinct Margin: D+21%	Voter 670's Neighborhood 45°18'50"N 93°35'25"W approx. 12619, Meadowvale Road Northwest, Elk River, Sherburne County, Minnesota, 55330, United States Precinct Margin: R+16%
Voter 671's Neighborhood 45°17'4"N 93°25'20"W approx. 17319, Sodium Street Northwest, Ramsey, Anoka County, Minnesota, 55303, United States Precinct Margin: R+16%	Voter 672's Neighborhood 35°2'39"N 106°29'46"W approx. 1108, Castellano Road Southeast, Four Hills (HOA), Albuquerque, Bernalillo County, New Mexico, 87123, United States Precinct Margin: R+9%
Voter 673's Neighborhood 40°40'42"N 112°0'6"W approx. 4698, Condie Park Circle, West Valley City, Salt Lake County, Utah, 84120, United States Precinct Margin: R+9%	Voter 674's Neighborhood 40°5'23"N 82°50'3"W approx. 5298, Hanover Close, Columbus, Sharon, Franklin County, Ohio, 43054, United States Precinct Margin: D+20%
Voter 675's Neighborhood 43°4'11"N 87°52'32"W approx. 2838, North Summit Avenue, Historic Water Tower Neighborhood, Milwaukee, Milwaukee County, Wisconsin, 53211, United States Precinct Margin: D+55%	Voter 676's Neighborhood 48°12'0"N 106°31'59"W approx. Pliley Road, Valley County, Montana, United States Precinct Margin: R+62%
Voter 677's Neighborhood 27°47'41"N 82°19'41"W approx. 10869, Candle Stick Lane, Hillsborough County, Florida, 33579, United States Precinct Margin: D+18%	Voter 678's Neighborhood 34°3'16"N 118°10'27"W approx. 1393, Machado Avenue, East Los Angeles, Los Angeles County, California, 90063, United States Precinct Margin: D+68%
Voter 679's Neighborhood 41°52'24"N 87°42'31"W approx. 3303-3305, West Harrison Street, East Garfield Park, Chicago, Cook County, Illinois, 60624, United States Precinct Margin: D+94%	Voter 680's Neighborhood 37°1'58"N 120°7'27"W approx. Avenue 19 1/2, Madera County, California, 93638-0299, United States Precinct Margin: D+1%
Voter 681's Neighborhood 38°38'56"N 90°15'36"W approx. 4750, Westminster Place, Central West End, Saint Louis, Missouri, 63108, United States Precinct Margin: D+75%	Voter 682's Neighborhood 40°28'37"N 88°54'8"W approx. 1370, South Towanda Barnes Road, McLean County, Illinois, 61704, United States Precinct Margin: R+31%
Voter 683's Neighborhood 44°36'44"N 75°10'34"W approx. Remington Recreation Trail, Canton, Town of Canton, Saint Lawrence County, New York, 13617, United States Precinct Margin: D+42%	Voter 684's Neighborhood 34°48'9"N 84°7'55"W approx. Benton MacKaye Trail, Union County, Georgia, United States Precinct Margin: R+66%
Voter 685's Neighborhood 34°13'33"N 80°17'38"W approx. 399, Traub Road, Lee County, South Carolina, 29010, United States Precinct Margin: D+10%	Voter 686's Neighborhood 32°15'48"N 90°7'24"W approx. 2388, Milam Street, Randall Place, Cunningham Heights, Pearl, Rankin County, Mississippi, 39208, United States Precinct Margin: R+37%
Voter 687's Neighborhood 35°20'46"N 80°39'7"W approx. 699, Pitts School Road Southwest, Concord, Cabarrus County, North Carolina, 28027, United States Precinct Margin: R+9%	Voter 688's Neighborhood 42°13'6"N 72°16'56"W approx. Palmer Wildlife Management Area, Rondeau Street, Palmer, Hampden County, Massachusetts, 01092, United States Precinct Margin: R+7%
Voter 689's Neighborhood 41°20'42"N 72°56'30"W approx. 63, Sunset Road, Pine Rock, Hamden, New Haven County, Connecticut, 06514, United States Precinct Margin: D+74%	Voter 690's Neighborhood 33°32'48"N 82°8'2"W approx. Columbia County Amphitheater, Evans Library Walking Path, Evans, Columbia County, Georgia, United States Precinct Margin: R+28%
Voter 691's Neighborhood 39°54'25"N 82°57'45"W approx. 1191, Evergreen Road, Columbus, Franklin County, Ohio, 43207, United States Precinct Margin: D+77%	Voter 692's Neighborhood 42°10'9"N 88°3'14"W approx. 21899, West Hidden Valley Road, Hidden Valley, Kildeer, Lake County, Illinois, 60047, United States Precinct Margin: R+1%
Voter 693's Neighborhood 35°51'52"N 80°59'32"W approx. 188, Liberty Hill Road, Statesville, Iredell County, North Carolina, 28625, United States Precinct Margin: R+54%	Voter 694's Neighborhood 41°53'40"N 88°1'52"W approx. 516, West Meadow Avenue, Lombard, DuPage County, Illinois, 60148, United States Precinct Margin: D+16%
Voter 695's Neighborhood 30°17'24"N 97°44'41"W approx. 2508, Rio Grande Street, The Drag, Austin, Travis County, Texas, 78705-5609, United States Precinct Margin: D+67%	Voter 696's Neighborhood 44°26'33"N 88°7'13"W approx. 1918, Sandy Springs Road, Town of Lawrence, Brown County, Wisconsin, 54115, United States Precinct Margin: R+23%
Voter 697's Neighborhood 33°56'56"N 117°46'53"W approx. 1099, Hillside Road, Chino Hills, San Bernardino County, California, 91709, United States Precinct Margin: R+9%	Voter 698's Neighborhood 31°17'56"N 92°37'8"W approx. 866, Belgard Bend Road, Rapides Parish, Louisiana, 71409, United States Precinct Margin: R+62%
Voter 699's Neighborhood 33°12'56"N 97°45'12"W approx. 1301, Irvin Street, Bridgeport, Wise County, Texas, 76426, United States Precinct Margin: R+53%	Voter 700's Neighborhood 36°34'23"N 121°37'37"W approx. 208, Pine Canyon Road, Monterey County, California, 93908, United States Precinct Margin: R+6%
Voter 701's Neighborhood 42°31'13"N 70°55'11"W approx. 24, Maple Street, Salem, Essex County, Massachusetts, 01970, United States Precinct Margin: D+41%	Voter 702's Neighborhood 38°28'59"N 81°53'21"W approx. 2133, Rocky Step Road, Black Lick Estates, Putnam County, West Virginia, 25560, United States Precinct Margin: R+37%
Voter 703's Neighborhood 41°7'34"N 77°28'27"W approx. 298, Birch Street, Flemington, Clinton County, Pennsylvania, 17745, United States Precinct Margin: R+27%	Voter 704's Neighborhood 44°0'51"N 88°35'39"W approx. 2352, Abbey Avenue, Oshkosh, Winnebago County, Wisconsin, 54904, United States Precinct Margin: D+15%
Voter 705's Neighborhood 35°8'51"N 101°53'20"W approx. 4806, Westway Trail, Amarillo, Randall County, Texas, 79109, United States Precinct Margin: R+49%	Voter 706's Neighborhood 37°21'52"N 122°11'22"W approx. Coyote Trail, Palo Alto, Santa Clara County, California, 94028, United States Precinct Margin: D+73%
Voter 707's Neighborhood 35°10'30"N 111°41'21"W approx. 2455, West Kiltie Lane, Equestrian Estates, Flagstaff, Coconino County, Arizona, 86005, United States Precinct Margin: D+30%	Voter 708's Neighborhood 26°15'34"N 98°16'2"W approx. Sharyland North Junior High School, 5100, Dove Avenue, McAllen, Hidalgo County, Texas, 78504, United States Precinct Margin: D+13%
Voter 709's Neighborhood 38°27'44"N 121°23'0"W approx. 8606, Delahye Circle, Elk Grove, Sacramento County, California, 95828, United States Precinct Margin: D+35%	Voter 710's Neighborhood 40°21'31"N 111°42'29"W approx. 1338, 500 South Drive, Pleasant Grove, Utah County, Utah, 84062, United States Precinct Margin: R+44%
Voter 711's Neighborhood 30°11'38"N 97°47'37"W approx. 7107, Cooper Lane, Austin, Travis County, Texas, 78745, United States Precinct Margin: D+65%	Voter 712's Neighborhood 35°19'29"N 97°25'24"W approx. 14460, South Sooner Road, Oklahoma City, Cleveland County, Oklahoma, 73165, United States Precinct Margin: R+43%
Voter 713's Neighborhood 45°4'26"N 93°15'7"W approx. 691, Marigold Terrace, Fridley, Anoka County, Minnesota, 55432, United States Precinct Margin: D+34%	Voter 714's Neighborhood 38°38'44"N 90°39'34"W approx. 18018, Wild Horse Creek Road, Wildwood, Saint Louis County, Missouri, 63005, United States Precinct Margin: R+19%
Voter 715's Neighborhood 38°39'9"N 76°57'43"W approx. 10159, Further Lane, Somerset, Waldorf, Charles County, Maryland, 20601, United States Precinct Margin: D+62%	Voter 716's Neighborhood 44°8'24"N 83°52'42"W approx. 1927, North Black Road, Mason Township, Arenac County, Michigan, 48766, United States Precinct Margin: R+43%
Voter 717's Neighborhood 37°45'11"N 122°14'52"W approx. Marsh Overlook, Alameda, Alameda County, California, 94501, United States Precinct Margin: D+69%	Voter 718's Neighborhood 40°6'16"N 82°50'0"W approx. Greenwyck Crossing, Columbus, Sharon, Franklin County, Ohio, 43054, United States Precinct Margin: D+20%
Voter 719's Neighborhood 41°24'20"N 71°42'48"W approx. White Trail, Charlestown, South County, Rhode Island, 02808, United States Precinct Margin: D+15%	Voter 720's Neighborhood 36°5'23"N 119°34'11"W approx. 1846, Josephine Avenue, Corcoran, Kings County, California, 93212, United States Precinct Margin: D+9%
Voter 721's Neighborhood 46°40'2"N 120°32'56"W approx. 1327, West Goodlander Road, Selah, Yakima County, Washington, 98942, United States Precinct Margin: R+24%	Voter 722's Neighborhood 37°31'49"N 94°18'6"W approx. 25, Northwest 20th Road, Wimmer, Barton County, Missouri, 64759, United States Precinct Margin: R+80%
Voter 723's Neighborhood 33°59'16"N 118°23'28"W approx. Hannum Avenue, Fox Hills, Culver City, Los Angeles County, California, 90230, United States Precinct Margin: D+68%	Voter 724's Neighborhood 35°23'2"N 78°32'52"W approx. 202, West Hill Street, Benson, Johnston County, North Carolina, 27504, United States Precinct Margin: R+46%
Voter 725's Neighborhood 41°19'55"N 96°10'24"W approx. North 165th Street, Summer Hill Farm, Douglas County, Nebraska, 68007, United States Precinct Margin: R+8%	Voter 726's Neighborhood 41°3'21"N 73°51'33"W approx. 2, Carriage Trail, Greystone on Hudson, Village of Tarrytown, Town of Greenburgh, Westchester County, New York, 10591, United States Precinct Margin: D+43%
Voter 727's Neighborhood 41°31'2"N 74°2'27"W approx. 89, Creek Run Road, Glenwood Park, Town of Newburgh, Orange County, New York, 12550, United States Precinct Margin: D+12%	Voter 728's Neighborhood 42°9'2"N 71°14'50"W approx. 13, School Street, Walpole, Norfolk County, Massachusetts, 02081, United States Precinct Margin: D+20%
Voter 729's Neighborhood 45°21'23"N 122°39'3"W approx. 23128, Bland Circle, Savannah Oaks, Willamette, West Linn, Clackamas County, Oregon, 97068, United States Precinct Margin: D+31%	Voter 730's Neighborhood 32°44'37"N 107°13'32"W approx. I 25, Derry, Sierra County, New Mexico, 87933, United States Precinct Margin: R+2%
Voter 731's Neighborhood 47°35'3"N 122°18'23"W approx. 2106, 20th Avenue South, Beacon Hill, Seattle, King County, Washington, 98144, United States Precinct Margin: D+63%	Voter 732's Neighborhood 38°58'1"N 90°59'56"W approx. 99, Southwest Lane, Troy, Lincoln County, Missouri, 63379, United States Precinct Margin: R+51%
Voter 733's Neighborhood 40°47'8"N 73°58'16"W approx. 38, West 86th Street, Upper West Side, Manhattan, New York County, City of New York, New York, 10024, United States Precinct Margin: D+79%	Voter 734's Neighborhood 44°50'16"N 93°18'54"W approx. 9146, Upton Avenue South, Bloomington, Hennepin County, Minnesota, 55431, United States Precinct Margin: D+30%
Voter 735's Neighborhood 30°13'26"N 89°46'40"W approx. Bayou Country General Store, East Howze Beach Road, Slidell, St. Tammany Parish, Louisiana, 70458, United States Precinct Margin: D+26%	Voter 736's Neighborhood 30°44'53"N 81°36'36"W approx. 573, East Cardinal Circle, St. Marys, Camden County, Georgia, 31558, United States Precinct Margin: R+43%
Voter 737's Neighborhood 41°41'10"N 88°10'38"W approx. 4431, Esquire Circle, River Run, Naperville, Will County, Illinois, 60564, United States Precinct Margin: D+17%	Voter 738's Neighborhood 26°32'24"N 81°55'23"W approx. 6913, Deep Lagoon Lane, Lee County, Florida, 33919, United States Precinct Margin: R+24%
Voter 739's Neighborhood 45°33'3"N 122°30'28"W approx. 3828, Northeast 149th Avenue, Wilkes, Portland, Multnomah County, Oregon, 97230, United States Precinct Margin: D+37%	Voter 740's Neighborhood 41°34'22"N 90°35'1"W approx. 5027, Brown Street, Colony Park, Davenport, Scott County, Iowa, 52806, United States Precinct Margin: D+18%
Voter 741's Neighborhood 35°6'15"N 106°32'22"W approx. 9412, Arvada Avenue Northeast, Mesa Village, Albuquerque, Bernalillo County, New Mexico, 87112, United States Precinct Margin: D+26%	Voter 742's Neighborhood 40°1'8"N 87°47'12"W approx. 10276, 800 East Road, Vermilion County, Illinois, 61841, United States Precinct Margin: R+52%
Voter 743's Neighborhood 37°47'10"N 122°24'15"W approx. Four Seasons, 757, Market Street, Union Square, San Francisco, California, 94103, United States Precinct Margin: D+52%	Voter 744's Neighborhood 39°11'47"N 76°38'39"W approx. 20, Archwood Avenue, Shirley Estates, Woodlawn Heights, Anne Arundel County, Maryland, 21061, United States Precinct Margin: R+20%
Voter 745's Neighborhood 26°8'28"N 80°13'17"W approx. 1382, Northwest 54th Avenue, Lauderhill, Sunrise, Broward County, Florida, 33313, United States Precinct Margin: D+88%	Voter 746's Neighborhood 44°53'54"N 93°3'24"W approx. 509, 18th Avenue North, South St. Paul, Dakota County, Minnesota, 55075, United States Precinct Margin: D+21%
Voter 747's Neighborhood 42°3'37"N 80°2'29"W approx. 359, Melvin Road, Proctor Heights, Summit Township, Erie County, Pennsylvania, 16509, United States Precinct Margin: R+10%	Voter 748's Neighborhood 42°9'19"N 121°39'34"W approx. 10699, Crystal Springs Road, Klamath County, Oregon, 97603, United States Precinct Margin: R+72%
Voter 749's Neighborhood 38°50'19"N 94°30'17"W approx. East 157th Street, Hardee Meadows, Belton, Cass County, Missouri, 64149, United States Precinct Margin: R+20%	Voter 750's Neighborhood 28°9'53"N 82°21'58"W approx. 20359, Starfinder Way, Tampa, Hillsborough County, Florida, 33647, United States Precinct Margin: D+39%
Voter 751's Neighborhood 39°12'2"N 84°33'25"W approx. 1950, Connecticut Avenue, College Hill, Cincinnati, Hamilton County, Ohio, 45224, United States Precinct Margin: D+64%	Voter 752's Neighborhood 35°56'21"N 82°5'1"W approx. 909, Pine Mountain Road, Minpro, Mitchell County, North Carolina, 28777, United States Precinct Margin: R+55%
Voter 753's Neighborhood 43°0'35"N 78°43'1"W approx. 101, Farmington Road, Woodstream Farms, Buffalo, Erie County, New York, 14221, United States Precinct Margin: D+9%	Voter 754's Neighborhood 41°12'3"N 96°12'41"W approx. 5790, South 190th Terrace, Douglas County, Nebraska, 68135, United States Precinct Margin: R+6%
Voter 755's Neighborhood 37°31'58"N 122°15'12"W approx. 564, Island Place, Redwood Shores, Redwood City, San Mateo County, California, 94065, United States Precinct Margin: D+55%	Voter 756's Neighborhood 27°3'31"N 82°21'31"W approx. 498, Cardiff Road, Sarasota County, Florida, 34293, United States Precinct Margin: R+20%
Voter 757's Neighborhood 35°28'45"N 97°29'34"W approx. The University of Oklahoma (Health Sciences Center), Northeast 13th Street, Oklahoma City, Oklahoma County, Oklahoma, 73117, United States Precinct Margin: D+49%	Voter 758's Neighborhood 39°50'15"N 86°8'37"W approx. 4489, Carrollton Avenue, Watson Park, Meridian Kessler, Indianapolis, Marion County, Indiana, 46205, United States Precinct Margin: D+78%
Voter 759's Neighborhood 41°20'2"N 74°10'57"W approx. 150, Franklin Avenue, Village of Monroe, Town of Monroe, Orange County, New York, 10950, United States Precinct Margin: D+3%	Voter 760's Neighborhood 40°49'22"N 84°55'18"W approx. 347, Stevenson Street, Decatur, Adams County, Indiana, 46733, United States Precinct Margin: R+27%
Voter 761's Neighborhood 35°41'26"N 105°56'58"W approx. 683, Jimenez Street, Santa Fe, Santa Fe County, New Mexico, 87501, United States Precinct Margin: D+84%	Voter 762's Neighborhood 36°6'42"N 97°7'4"W approx. 920, South Murphy Street, Tradan Heights, Stillwater, Payne County, Oklahoma, 74074, United States Precinct Margin: R+7%
Voter 763's Neighborhood 34°14'1"N 118°31'38"W approx. 18101, Osborne Street, Northridge, Los Angeles, Los Angeles County, California, 91325, United States Precinct Margin: D+42%	Voter 764's Neighborhood 35°14'25"N 89°30'39"W approx. Fair Oaks Golf Course, Wirt Road, Oakland, Fayette County, Tennessee, 38060, United States Precinct Margin: R+38%
Voter 765's Neighborhood 42°25'29"N 83°6'28"W approx. 461, Erle Street, Grixdale Farms, Detroit, Wayne County, Michigan, 48203, United States Precinct Margin: D+87%	Voter 766's Neighborhood 44°51'11"N 93°26'52"W approx. 13444, Winchester Place, Eden Prairie, Hennepin County, Minnesota, 55344, United States Precinct Margin: D+41%
Voter 767's Neighborhood 41°52'56"N 87°48'8"W approx. 352, Wisconsin Avenue, Samuel A Rothermel Houses, Oak Park, Cook County, Illinois, 60302, United States Precinct Margin: D+78%	Voter 768's Neighborhood 41°44'55"N 91°35'51"W approx. Sugar Bottom Bikes, 325, North Dubuque Street, North Liberty, Johnson County, Iowa, 52317, United States Precinct Margin: D+31%
Voter 769's Neighborhood 38°32'53"N 106°55'41"W approx. 447, North Wisconsin Street, Gunnison, Gunnison County, Colorado, 81230, United States Precinct Margin: D+40%	Voter 770's Neighborhood 34°2'36"N 86°2'16"W approx. 823, Hinds Road, The Highlands, Gadsden, Etowah County, Alabama, 35904, United States Precinct Margin: R+50%
Voter 771's Neighborhood 39°57'53"N 74°58'54"W approx. 698, Grand Avenue, Lenola, Moorestown Township, Burlington County, New Jersey, 08057, United States Precinct Margin: D+23%	Voter 772's Neighborhood 43°0'25"N 73°42'36"W approx. 50, Putnam Road, Wayville, Town of Stillwater, Town of Saratoga, Saratoga County, New York, 12170, United States Precinct Margin: R+16%
Voter 773's Neighborhood 41°51'39"N 88°6'57"W approx. 557, South Carlton Avenue, Wheaton, DuPage County, Illinois, 60187, United States Precinct Margin: D+32%	Voter 774's Neighborhood 41°9'32"N 96°0'24"W approx. 2120, Leigh Street, Papillion, Sarpy County, Nebraska, 68133, United States Precinct Margin: R+13%
Voter 775's Neighborhood 42°51'47"N 93°38'10"W approx. 2747, 130th Street, Wright County, Iowa, 50421, United States Precinct Margin: R+26%	Voter 776's Neighborhood 42°16'5"N 88°11'12"W approx. East State Road, Island Lake, Lake County, Illinois, 60042, United States Precinct Margin: D+6%
Voter 777's Neighborhood 38°3'10"N 91°29'29"W approx. 5549, Old Springfield Road, Crawford County, Missouri, 65453, United States Precinct Margin: R+61%	Voter 778's Neighborhood 38°13'46"N 122°35'53"W approx. 77, Cader Lane, Petaluma, Sonoma County, California, 94954, United States Precinct Margin: D+56%
Voter 779's Neighborhood 39°49'7"N 75°8'1"W approx. 601, South Barlow Avenue, Deptford, Deptford Township, Gloucester County, New Jersey, 08096, United States Precinct Margin: D+13%	Voter 780's Neighborhood 33°40'17"N 84°58'59"W approx. 154, Martin Road, Carroll County, Georgia, 30116, United States Precinct Margin: R+45%
Voter 781's Neighborhood 32°48'51"N 116°55'52"W approx. 1346, Groveland Terrace, Bostonia, El Cajon, San Diego County, California, 92021, United States Precinct Margin: R+13%	Voter 782's Neighborhood 41°19'17"N 96°9'31"W approx. Gilbert Boarding Kennels, 6904, North 156th Street, Bennington, Douglas County, Nebraska, 68007, United States Precinct Margin: R+9%
Voter 783's Neighborhood 27°22'3"N 82°30'38"W approx. 3705, Voorne Street, Beverley Terrace, Sarasota County, Florida, 34234, United States Precinct Margin: R+15%	Voter 784's Neighborhood 31°22'11"N 84°55'48"W approx. 253, Lancelot Lane, Blakely, Early County, Georgia, 39823, United States Precinct Margin: D+27%
Voter 785's Neighborhood 47°32'20"N 122°16'13"W approx. Myrtle Street Apartments, South Myrtle Street, Brighton Beach, Seattle, King County, Washington, 98118, United States Precinct Margin: D+69%	Voter 786's Neighborhood 33°20'39"N 92°39'26"W approx. 897, Hayes City Road, Union County, Arkansas, 71762, United States Precinct Margin: R+66%
Voter 787's Neighborhood 38°40'16"N 121°46'33"W approx. 732, Dingle Lane, Woodland, Yolo County, California, 95695, United States Precinct Margin: D+18%	Voter 788's Neighborhood 25°41'6"N 80°28'12"W approx. Southwest 88th Street, Miami-Dade County, Florida, 33176, United States Precinct Margin: R+5%
Voter 789's Neighborhood 40°42'54"N 73°57'42"W approx. 136, North 1st Street, Brooklyn, Kings County, City of New York, New York, 11249, United States Precinct Margin: D+77%	Voter 790's Neighborhood 33°13'33"N 86°55'1"W approx. Coalmont Road, Coalmont, Helena, Shelby County, Alabama, 35080, United States Precinct Margin: R+39%
Voter 791's Neighborhood 38°57'3"N 76°46'3"W approx. Warners Discovery Way, Fairwood, Prince George's County, Maryland, United States Precinct Margin: D+84%	Voter 792's Neighborhood 39°17'12"N 83°58'52"W approx. South Wright Street, Blanchester, Clinton County, Ohio, 45107, United States Precinct Margin: R+66%
Voter 793's Neighborhood 35°47'49"N 78°31'45"W approx. Coffey Street, Green Pines, Milburnie, Wake County, North Carolina, 27604, United States Precinct Margin: D+36%	Voter 794's Neighborhood 42°33'42"N 71°1'38"W approx. 5, Surrey Lane, Peabody, Essex County, Massachusetts, 01949, United States Precinct Margin: R+3%
Voter 795's Neighborhood 41°11'25"N 73°16'2"W approx. 381, Hollydale Road, Fairfield, Fairfield County, Connecticut, 06824, United States Precinct Margin: D+24%	Voter 796's Neighborhood 37°23'14"N 93°8'19"W approx. 537, Cottonwood Street, Fair Grove, Greene County, Missouri, 65648, United States Precinct Margin: R+52%
Voter 797's Neighborhood 33°8'27"N 117°4'19"W approx. 1219, Armstrong Circle, Escondido, San Diego County, California, 92027, United States Precinct Margin: D+35%	Voter 798's Neighborhood 34°56'10"N 89°57'27"W approx. 5298, Iraon Circle, Southaven, DeSoto County, Mississippi, 38671, United States Precinct Margin: R+30%
Voter 799's Neighborhood 41°9'32"N 96°0'24"W approx. 2120, Leigh Street, Papillion, Sarpy County, Nebraska, 68133, United States Precinct Margin: R+13%	Voter 800's Neighborhood 41°52'52"N 88°1'15"W approx. 199, West Willow Street, Lombard, DuPage County, Illinois, 60148, United States Precinct Margin: D+28%
Voter 801's Neighborhood 40°2'27"N 75°24'16"W approx. Warren Filipone Memorial Park Tennis Courts, South Devon Avenue, West Wayne, Wayne, Radnor Township, Delaware County, Pennsylvania, 19087-3305, United States Precinct Margin: D+38%	Voter 802's Neighborhood 42°37'48"N 70°38'45"W approx. 12, Heritage Way, Gloucester, Essex County, Massachusetts, 01930-3540, United States Precinct Margin: D+37%
Voter 803's Neighborhood 40°10'14"N 105°5'27"W approx. Kensington Ditch Trail, Longmont, Boulder County, Colorado, 80501-4919, United States Precinct Margin: D+45%	Voter 804's Neighborhood 39°3'24"N 76°59'9"W approx. Jackson Road, East Springbrook, White Oak, Montgomery County, Maryland, 20904, United States Precinct Margin: D+67%
Voter 805's Neighborhood 33°11'19"N 97°7'3"W approx. 1881, Concord Lane, Denton, Denton County, Texas, 76205, United States Precinct Margin: R+7%	Voter 806's Neighborhood 38°41'32"N 121°47'13"W approx. 69, West Kentucky Avenue, Woodland, Yolo County, California, 95695, United States Precinct Margin: D+27%
Voter 807's Neighborhood 40°53'18"N 73°7'16"W approx. 25, Annandale Road, Suffolk County, New York, 11790, United States Precinct Margin: D+11%	Voter 808's Neighborhood 37°59'38"N 81°7'29"W approx. 941, Gatewood Road, East Oak Hill, Oak Hill, Fayette County, West Virginia, 25840, United States Precinct Margin: R+49%
Voter 809's Neighborhood 44°35'12"N 123°15'54"W approx. Linus Pauling Middle School, Northwest Cleveland Avenue, Corvallis, Benton County, Oregon, 97330, United States Precinct Margin: D+62%	Voter 810's Neighborhood 32°54'14"N 79°49'14"W approx. 2318, Kings Gate Lane, Mount Pleasant, Charleston County, South Carolina, 29466, United States Precinct Margin: R+25%
Voter 811's Neighborhood 26°6'4"N 80°12'40"W approx. 1561, Southwest 46th Avenue, Fern Crest Village, Broadview Park, Sunrise, Broward County, Florida, 33317, United States Precinct Margin: D+13%	Voter 812's Neighborhood 40°2'9"N 86°1'10"W approx. 399, Chestnut Street, Noblesville, Hamilton County, Indiana, 46060, United States Precinct Margin: R+28%
Voter 813's Neighborhood 44°49'47"N 93°15'11"W approx. 1526, East 96th Street, Bloomington, Hennepin County, Minnesota, 55425, United States Precinct Margin: D+18%	Voter 814's Neighborhood 41°52'27"N 84°4'19"W approx. 2573, West Cadmus Road, Madison Township, Lenawee County, Michigan, 49221, United States Precinct Margin: R+41%
Voter 815's Neighborhood 39°34'34"N 104°53'12"W approx. 8745, East Kettle Place, Centennial, Arapahoe County, Colorado, 80112, United States Precinct Margin: D+28%	Voter 816's Neighborhood 44°53'51"N 123°6'41"W approx. River Road South, Salem, Marion County, Oregon, United States Precinct Margin: D+26%
Voter 817's Neighborhood 42°13'51"N 72°19'40"W approx. Herman Covey Wildlife Management Area, Bondsville Road, Ware, Hampshire County, Massachusetts, 01009, United States Precinct Margin: R+9%	Voter 818's Neighborhood 30°40'22"N 94°45'34"W approx. Pauline Avenue, Polk County, Texas, United States Precinct Margin: R+72%
Voter 819's Neighborhood 35°51'1"N 79°10'51"W approx. 191, Wild Rose Lane, Town of Pittsboro, Chatham County, North Carolina, 27312, United States Precinct Margin: D+45%	Voter 820's Neighborhood 39°35'48"N 76°54'5"W approx. 2610, Shiloh Road, Shiloh, Carroll County, Maryland, 21074, United States Precinct Margin: R+38%
Voter 821's Neighborhood 39°10'45"N 77°5'43"W approx. Our House Residential Job Training Center For Youth, Olney Laytonsville Road, Olney, Montgomery County, Maryland, 20832, United States Precinct Margin: D+27%	Voter 822's Neighborhood 38°8'51"N 75°45'36"W approx. Mount Olive Cemetery, Revells Neck Road, Somerset County, Maryland, 21890, United States Precinct Margin: R+58%
Voter 823's Neighborhood 42°58'47"N 83°42'31"W approx. 1343, Lynton Avenue, Flint, Genesee County, Michigan, 48507, United States Precinct Margin: D+14%	Voter 824's Neighborhood 34°47'21"N 97°36'11"W approx. N3022 Road, Garvin County, Oklahoma, United States Precinct Margin: R+80%
Voter 825's Neighborhood 39°12'38"N 84°35'56"W approx. 3533, Blue Rock Road, White Oak, Colerain Township, Hamilton County, Ohio, 45247, United States Precinct Margin: R+5%	Voter 826's Neighborhood 35°23'12"N 80°41'35"W approx. 598, Pitts School Road Northwest, Riverwalk, Concord, Cabarrus County, North Carolina, 28027, United States Precinct Margin: R+7%
Voter 827's Neighborhood 28°55'56"N 81°45'14"W approx. 11914, Lizard Lane, Lake County, Florida, 32784, United States Precinct Margin: R+36%	Voter 828's Neighborhood 42°18'37"N 122°49'43"W approx. The Church of Jesus Christ of Latter-day Saints, 2900, Juanipero Way, Medford, Jackson County, Oregon, 97504, United States Precinct Margin: D+8%
Voter 829's Neighborhood 38°10'14"N 77°37'47"W approx. Dixon Lane, Spotsylvania County, Virginia, 22551, United States Precinct Margin: R+15%	Voter 830's Neighborhood 42°10'2"N 83°23'57"W approx. Albert Lane, New Boston, Huron Township, Wayne County, Michigan, United States Precinct Margin: R+30%
Voter 831's Neighborhood 45°0'5"N 84°39'6"W approx. 516, West McCoy Road, Gaylord, Bagley Township, Otsego County, Michigan, 49735, United States Precinct Margin: R+36%	Voter 832's Neighborhood 33°24'7"N 86°52'46"W approx. 1593, Melton Road, Shannon, Hoover, Jefferson County, Alabama, 35022, United States Precinct Margin: R+8%
Voter 833's Neighborhood 41°54'53"N 74°2'23"W approx. Wiltwyck Golf Club, 404, Stewart Lane, City of Kingston, Town of Ulster, Ulster County, New York, 12401, United States Precinct Margin: D+17%	Voter 834's Neighborhood 45°12'51"N 93°15'24"W approx. 563, 134th Lane Northeast, Ham Lake, Anoka County, Minnesota, 55304, United States Precinct Margin: R+23%
Voter 835's Neighborhood 43°9'1"N 76°20'36"W approx. 111, Pebblewood Ln, Village of Baldwinsville, Town of Van Buren, Onondaga County, New York, 13027, United States Precinct Margin: D+15%	Voter 836's Neighborhood 37°18'13"N 79°58'1"W approx. 4882, Ring Road Northwest, Fairland, Roanoke, Virginia, 24012, United States Precinct Margin: D+31%
Voter 837's Neighborhood 34°15'48"N 118°27'7"W approx. 14674, Kingsbury Street, Los Angeles, Los Angeles County, California, 91345, United States Precinct Margin: D+47%	Voter 838's Neighborhood 33°22'28"N 117°12'56"W approx. 552, Tumble Creek Terrace, Fallbrook, San Diego County, California, 92028, United States Precinct Margin: R+18%
Voter 839's Neighborhood 29°53'9"N 97°57'23"W approx. 999, North Loop Street, San Marcos, Hays County, Texas, 78666, United States Precinct Margin: D+46%	Voter 840's Neighborhood 33°42'0"N 117°57'20"W approx. Orange Coast Memorial Medical Center, 18111, Brookhurst Street, Fountain Valley, Orange County, California, 92708, United States Precinct Margin: D+3%
Voter 841's Neighborhood 32°37'59"N 83°46'31"W approx. 2531, Powersville Road, Powersville, Peach County, Georgia, 31008, United States Precinct Margin: R+25%	Voter 842's Neighborhood 33°45'29"N 117°47'43"W approx. 1291, Banbury Cross Road, Lemon Heights, North Tustin, Orange, Orange County, California, 92705, United States Precinct Margin: R+13%
Voter 843's Neighborhood 40°42'19"N 73°48'14"W approx. 88-02, 153rd Street, Jamaica, Queens, City of New York, New York, 11432, United States Precinct Margin: D+79%	Voter 844's Neighborhood 41°53'44"N 87°38'17"W approx. Superior House, 366, West Superior Street, River North, Near North Side, Chicago, Cook County, Illinois, 60654, United States Precinct Margin: D+50%
Voter 845's Neighborhood 41°34'48"N 93°48'18"W approx. 860, 71st Street, Reed's Crossing, West Des Moines, Dallas County, Iowa, 50266, United States Precinct Margin: D+11%	Voter 846's Neighborhood 41°32'0"N 75°59'10"W approx. Lake Wilderness Road, Wyoming County, Pennsylvania, 18657, United States Precinct Margin: R+30%
Voter 847's Neighborhood 40°23'14"N 122°29'6"W approx. 3316, Hunter Road, Shasta County, California, 96022, United States Precinct Margin: R+53%	Voter 848's Neighborhood 44°49'26"N 122°58'58"W approx. 8771, Parrish Gap Road Southeast, Marion County, Oregon, 97392, United States Precinct Margin: R+33%
Voter 849's Neighborhood 40°43'16"N 74°12'40"W approx. University High School, Millington Avenue, Newark, Essex County, New Jersey, 07108, United States Precinct Margin: D+90%	Voter 850's Neighborhood 33°55'35"N 118°15'28"W approx. 954, East 118th Street, Green Meadows, Los Angeles, Los Angeles County, California, 90059, United States Precinct Margin: D+70%
Voter 851's Neighborhood 42°14'55"N 83°38'28"W approx. 1850, Whittier Road, College Heights, Ypsilanti, Washtenaw County, Michigan, 48197, United States Precinct Margin: D+69%	Voter 852's Neighborhood 39°26'4"N 77°49'10"W approx. Walgreens, Martinsburg Pike, Shepherdstown, Jefferson County, West Virginia, 25443, United States Precinct Margin: D+33%
Voter 853's Neighborhood 29°31'17"N 98°21'27"W approx. Crestway Road, Windcrest, Bexar County, Texas, 78239, United States Precinct Margin: D+24%	Voter 854's Neighborhood 30°11'50"N 93°10'32"W approx. Lake Charles Loop, Greinwich Village, Lake Charles, Calcasieu Parish, Louisiana, 70602, United States Precinct Margin: D+88%
Voter 855's Neighborhood 38°51'41"N 77°15'24"W approx. Chichester's Mill Race, Cross County Trail, Mantua, Fairfax County, Virginia, 22031, United States Precinct Margin: D+39%	Voter 856's Neighborhood 29°6'14"N 82°4'6"W approx. 46, Juniper Loop Way, Marion County, Florida, 34480, United States Precinct Margin: R+22%
Voter 857's Neighborhood 40°23'11"N 74°7'8"W approx. 15, Wychwood Road, Middletown, Middletown Township, Monmouth County, New Jersey, 07748, United States Precinct Margin: R+11%	Voter 858's Neighborhood 42°26'9"N 71°5'3"W approx. 23, McCormack Street, Malden Highlands, Malden, Middlesex County, Massachusetts, 02176-6104, United States Precinct Margin: D+50%
Voter 859's Neighborhood 41°22'10"N 81°20'0"W approx. 8658, Taylor May Road, Bainbridge Township, Geauga County, Ohio, 44023, United States Precinct Margin: R+7%	Voter 860's Neighborhood 40°6'34"N 75°54'2"W approx. 74, Todd Road, Honey Brook Township, Chester County, Pennsylvania, 19344, United States Precinct Margin: R+30%
Voter 861's Neighborhood 33°24'54"N 79°57'45"W approx. State Highway 45, Old Peru, Berkeley County, South Carolina, 29468, United States Precinct Margin: D+65%	Voter 862's Neighborhood 29°12'7"N 82°3'28"W approx. Silver Springs Conservation Area, Northeast 51st Avenue, Marion County, Florida, 34470, United States Precinct Margin: R+40%
Voter 863's Neighborhood 47°57'15"N 117°25'2"W approx. 307, West Deer Park-Milan Road, Spokane County, Washington, 99006, United States Precinct Margin: R+42%	Voter 864's Neighborhood 43°9'45"N 93°9'28"W approx. 2572, 12th Street Northeast, College Heights, Mason City, Cerro Gordo County, Iowa, 50401, United States Precinct Margin: D+0%
Voter 865's Neighborhood 41°54'59"N 87°42'0"W approx. 1927, North Richmond Street, Logan Square, Chicago, Cook County, Illinois, 60647, United States Precinct Margin: D+77%	Voter 866's Neighborhood 33°30'14"N 112°1'25"W approx. Camelback High School, East Campbell Avenue, Camelback East, Phoenix, Maricopa County, Arizona, 85018-8830, United States Precinct Margin: D+14%
Voter 867's Neighborhood 42°59'23"N 72°42'53"W approx. 196, Hobby Hill Road, Newfane, Windham County, Vermont, 05345, United States Precinct Margin: D+51%	Voter 868's Neighborhood 39°46'56"N 75°53'16"W approx. 97, Hollow Rock Lane, New London, New London Township, Chester County, Pennsylvania, 19352, United States Precinct Margin: D+0%
Voter 869's Neighborhood 40°55'46"N 90°19'42"W approx. 3198, Grand Avenue, Galesburg, Knox County, Illinois, 61401, United States Precinct Margin: D+10%	Voter 870's Neighborhood 42°24'33"N 75°49'31"W approx. Upper Round Pond Road, Smithville Flats, Town of Smithville, Chenango County, New York, 13841, United States Precinct Margin: R+34%
Voter 871's Neighborhood 40°14'21"N 75°33'30"W approx. Pottstown Heritage Field, 3310, West Ridge Pike, Limerick, Limerick Township, Montgomery County, Pennsylvania, 19464, United States Precinct Margin: D+11%	Voter 872's Neighborhood 36°9'58"N 80°20'20"W approx. 4015, Talcott Avenue, Old Town, Winston-Salem, Forsyth County, North Carolina, 27106, United States Precinct Margin: D+17%
Voter 873's Neighborhood 38°42'18"N 75°6'31"W approx. 52, Windsor Road, Rehoboth Beach Yacht & Country Club, Silver View Farm, Sussex County, Delaware, 19971, United States Precinct Margin: D+24%	Voter 874's Neighborhood 30°26'46"N 97°49'42"W approx. 10801, Foundation Road, Austin, Travis County, Texas, 78726, United States Precinct Margin: D+36%
Voter 875's Neighborhood 37°42'53"N 122°26'25"W approx. 10, Curtis Street, Crocker-Amazon, San Francisco, California, 94112, United States Precinct Margin: D+57%	Voter 876's Neighborhood 29°51'52"N 95°35'57"W approx. 12798, Watercress Park, Villages at Lakepointe, Harris County, Texas, 77041, United States Precinct Margin: D+8%
Voter 877's Neighborhood 26°42'57"N 80°9'34"W approx. Riverwalk Circle, Riverwalk, West Palm Beach, Palm Beach County, Florida, United States Precinct Margin: R+1%	Voter 878's Neighborhood 46°48'39"N 95°50'13"W approx. 1298, Richard Avenue, Detroit Lakes, Becker County, Minnesota, 56501, United States Precinct Margin: R+8%
Voter 879's Neighborhood 39°44'35"N 105°1'54"W approx. 1615, Julian Street, West Colfax, Denver, Colorado, 80204, United States Precinct Margin: D+64%	Voter 880's Neighborhood 32°13'25"N 80°58'27"W approx. 198, Scarlet Oak, Meadows at New Riverside, Beaufort County, South Carolina, 29910, United States Precinct Margin: R+20%
Voter 881's Neighborhood 33°32'9"N 112°3'59"W approx. 496, East Lamar Road, Phoenix, Maricopa County, Arizona, 85012, United States Precinct Margin: D+13%	Voter 882's Neighborhood 40°25'9"N 101°18'34"W approx. Avenue 348 A, Hayes County, Nebraska, United States Precinct Margin: R+83%
Voter 883's Neighborhood 42°15'49"N 72°10'16"W approx. 58, John Gilbert Road, West Brookfield, Worcester County, Massachusetts, 01585, United States Precinct Margin: D+0%	Voter 884's Neighborhood 39°32'30"N 87°7'29"W approx. INDIANA OXIDE CORP, North Forest Avenue, Brazil, Brazil Township, Clay County, Indiana, 47834, United States Precinct Margin: R+54%
Voter 885's Neighborhood 40°42'34"N 111°49'48"W approx. 2130, Atkin Avenue, Canyon Rim, Millcreek, Salt Lake County, Utah, 84109, United States Precinct Margin: D+36%	Voter 886's Neighborhood 43°4'58"N 94°15'2"W approx. 220th Street, Algona, Kossuth County, Iowa, 50511, United States Precinct Margin: R+25%
Voter 887's Neighborhood 41°41'5"N 71°31'12"W approx. 109, Church Street, Centerville, Crompton, West Warwick, Kent County, Rhode Island, 02893, United States Precinct Margin: D+6%	Voter 888's Neighborhood 38°22'34"N 75°8'56"W approx. 11798, Manklin Creek Road, Ocean Pines, Worcester County, Maryland, 21811, United States Precinct Margin: R+12%
Voter 889's Neighborhood 33°37'32"N 117°51'25"W approx. 1842, Port Margate Place, Newport Center, Newport Beach, Orange County, California, 92660, United States Precinct Margin: R+11%	Voter 890's Neighborhood 39°38'20"N 84°13'13"W approx. Extended Stay America Dayton South, Lois Circle, Shanersville, Miami Township, Montgomery County, Ohio, 45459, United States Precinct Margin: R+20%
Voter 891's Neighborhood 41°41'3"N 86°14'41"W approx. 620, North Niles Avenue, South Bend, Saint Joseph County, Indiana, 46617, United States Precinct Margin: D+52%	Voter 892's Neighborhood 38°28'35"N 90°12'40"W approx. 320, Brellinger St, Brellinger Estates, Columbia, Monroe County, Illinois, 62236, United States Precinct Margin: R+20%
Voter 893's Neighborhood 40°16'0"N 75°12'34"W approx. 121, Cambridge Place, New Britain Walk, New Britain Township, Bucks County, Pennsylvania, 18914, United States Precinct Margin: D+7%	Voter 894's Neighborhood 38°46'8"N 77°13'14"W approx. School Track, Dog Walking Path, West Springfield, Fairfax County, Virginia, 22152, United States Precinct Margin: D+45%
Voter 895's Neighborhood 40°8'34"N 105°6'32"W approx. 891, Quebec Avenue, Longmont, Boulder County, Colorado, 80501, United States Precinct Margin: D+37%	Voter 896's Neighborhood 41°41'27"N 72°24'9"W approx. 343, East Street, Hebron, Tolland County, Connecticut, 06248, United States Precinct Margin: D+10%
Voter 897's Neighborhood 40°56'46"N 73°57'42"W approx. 325, Piermont Road, Cresskill, Bergen County, New Jersey, 07626, United States Precinct Margin: D+16%	Voter 898's Neighborhood 34°33'27"N 112°20'22"W approx. 7210, East Sienna Springs Lane, Prescott Valley, Yavapai County, Arizona, 86314, United States Precinct Margin: R+39%
Voter 899's Neighborhood 41°25'26"N 81°27'28"W approx. 5012, Crofton Avenue, Solon, Cuyahoga County, Ohio, 44139, United States Precinct Margin: D+40%	Voter 900's Neighborhood 35°36'27"N 82°25'55"W approx. Upper River Trail, Buncombe County, North Carolina, 28778, United States Precinct Margin: D+12%
Voter 901's Neighborhood 39°4'49"N 94°32'48"W approx. True Vine Baptist Church, East 25th Street, Washington Wheatley, Kansas City, Jackson County, Missouri, 64127, United States Precinct Margin: D+89%	Voter 902's Neighborhood 39°55'44"N 104°58'33"W approx. 12840, Clarkson Circle, Hunters Glen Lakeshore, Thornton, Adams County, Colorado, 80241, United States Precinct Margin: D+12%
Voter 903's Neighborhood 34°1'42"N 84°12'50"W approx. 368, Dewpoint Lane, Johns Creek, Fulton County, Georgia, 30022, United States Precinct Margin: R+2%	Voter 904's Neighborhood 30°28'35"N 85°7'23"W approx. 16795, Northwest Magnolia Church Road, Calhoun County, Florida, 32421, United States Precinct Margin: R+65%
Voter 905's Neighborhood 30°0'36"N 81°32'12"W approx. Leo Maguire Road, Elwood, Saint Johns County, Florida, 32092, United States Precinct Margin: R+32%	Voter 906's Neighborhood 39°47'9"N 75°37'13"W approx. 62, Westbrae Lane, New Castle County, Delaware, 19807, United States Precinct Margin: D+21%
Voter 907's Neighborhood 30°26'26"N 87°12'3"W approx. 1565, East Scott Street, Pensacola, Escambia County, Florida, 32503, United States Precinct Margin: D+15%	Voter 908's Neighborhood 37°3'2"N 94°30'4"W approx. 1398, East 34th Street, Dennis Acres, Joplin, Newton County, Missouri, 64804, United States Precinct Margin: R+37%
Voter 909's Neighborhood 34°11'57"N 118°24'42"W approx. 7095, Goodland Avenue, Valley Glen, Los Angeles, Los Angeles County, California, 91605, United States Precinct Margin: D+41%	Voter 910's Neighborhood 41°11'18"N 111°55'55"W approx. 1808, Acorn Circle, Ogden, Weber County, Utah, 84403, United States Precinct Margin: D+3%
Voter 911's Neighborhood 36°11'37"N 115°14'23"W approx. 1999, Joliet Circle, Inner Northwest, Las Vegas, Clark County, Nevada, 89108, United States Precinct Margin: D+33%	Voter 912's Neighborhood 37°9'47"N 94°40'52"W approx. Southeast Wyandotte Road, Cherokee County, Kansas, 66728, United States Precinct Margin: R+63%
Voter 913's Neighborhood 37°33'51"N 121°52'56"W approx. 3735, Andrade Road, Alameda County, California, 94586, United States Precinct Margin: D+23%	Voter 914's Neighborhood 34°26'49"N 83°48'51"W approx. 5481, Northwoods Road, Hall County, Georgia, 30527, United States Precinct Margin: R+75%
Voter 915's Neighborhood 42°32'1"N 90°50'13"W approx. 17897, Brehm Lane, Dubuque County, Iowa, 52002, United States Precinct Margin: R+14%	Voter 916's Neighborhood 40°41'26"N 73°42'59"W approx. 8, Frick Street, Alden Manor, Town of Hempstead, Nassau County, New York, 11003, United States Precinct Margin: D+80%
Voter 917's Neighborhood 31°45'58"N 89°10'24"W approx. 3, Greenbriar Lane, Jones County, Mississippi, 39440, United States Precinct Margin: R+40%	Voter 918's Neighborhood 35°44'5"N 81°25'25"W approx. 9094, Arary Est Road, Hildebran, Burke County, North Carolina, 28612, United States Precinct Margin: R+58%
Voter 919's Neighborhood 42°36'10"N 82°51'48"W approx. Elmo Street, Clemens Park, Charter Township of Clinton, Clinton Township, Macomb County, Michigan, 48043-5640, United States Precinct Margin: D+0%	Voter 920's Neighborhood 42°2'8"N 91°42'26"W approx. Saint Lukes Northridge Family Medicine, South Blairsferry Crossing, Heritage Creek, Cedar Rapids, Hiawatha, Linn County, Iowa, 52233, United States Precinct Margin: D+8%
Voter 921's Neighborhood 33°43'19"N 84°11'9"W approx. 2399, Creekview Trail, DeKalb County, Georgia, 30035, United States Precinct Margin: D+92%	Voter 922's Neighborhood 39°3'52"N 104°48'36"W approx. Forest Chime Place, El Paso County, Colorado, 80132-7725, United States Precinct Margin: R+32%
Voter 923's Neighborhood 41°52'8"N 84°46'36"W approx. 8494, Quackenbush Road, Reading Township, Hillsdale County, Michigan, 49274, United States Precinct Margin: R+39%	Voter 924's Neighborhood 40°46'6"N 76°19'10"W approx. 1090, Beaver Dam Road, Butler Township, Schuylkill County, Pennsylvania, 17921, United States Precinct Margin: R+44%
Voter 925's Neighborhood 29°49'23"N 95°11'45"W approx. Crosby Freeway Frontage Road, Beaumont Place, Harris County, Texas, 77049, United States Precinct Margin: D+53%	Voter 926's Neighborhood 32°28'6"N 86°17'37"W approx. 5237, Coosada Ferry Road, Montgomery, Montgomery County, Alabama, 36110, United States Precinct Margin: R+13%
Voter 927's Neighborhood 42°15'35"N 85°37'59"W approx. 3565, Parkview Avenue, Kalamazoo, Oshtemo Township, Kalamazoo County, Michigan, 49008, United States Precinct Margin: D+44%	Voter 928's Neighborhood 39°29'15"N 77°56'2"W approx. 98, Trafalgar Circle, Princeton Shoals, Martinsburg, Berkeley County, West Virginia, 25404, United States Precinct Margin: R+31%
Voter 929's Neighborhood 38°48'51"N 104°46'23"W approx. 1180, Server Drive, Colorado Springs, El Paso County, Colorado, 80910, United States Precinct Margin: D+13%	Voter 930's Neighborhood 30°29'24"N 90°26'42"W approx. 17090, Parker Lane, Hammond, Tangipahoa Parish, Louisiana, 70403, United States Precinct Margin: R+43%
Voter 931's Neighborhood 37°18'34"N 121°46'45"W approx. Evergreen Elementary School, 3010, Fowler Road, Evergreen, San Jose, Santa Clara County, California, 95135, United States Precinct Margin: D+45%	Voter 932's Neighborhood 33°4'58"N 117°3'46"W approx. 410, Park Ranch Place, Escondido, San Diego County, California, 92025, United States Precinct Margin: D+2%
Voter 933's Neighborhood 43°20'29"N 72°7'5"W approx. 101, Nutting Road, Sunapee, Sullivan County, New Hampshire, 03782, United States Precinct Margin: D+9%	Voter 934's Neighborhood 32°54'40"N 117°5'20"W approx. 10455, Mountain Glen Terrace, San Diego, San Diego County, California, 92131, United States Precinct Margin: D+25%
Voter 935's Neighborhood 44°4'36"N 93°12'24"W approx. 844, Minnesota Avenue, Owatonna, Steele County, Minnesota, 55060, United States Precinct Margin: R+19%	Voter 936's Neighborhood 30°27'18"N 91°1'39"W approx. 14019, Katherine Avenue, Sherwood Garden Homes, Baton Rouge, East Baton Rouge Parish, Louisiana, 70815, United States Precinct Margin: D+29%
Voter 937's Neighborhood 38°34'48"N 121°27'29"W approx. Blues Alley, Sacramento, Sacramento County, California, 95816, United States Precinct Margin: D+59%	Voter 938's Neighborhood 35°0'14"N 79°48'6"W approx. 547, Dockery Road, Richmond County, North Carolina, 28379, United States Precinct Margin: R+30%
Voter 939's Neighborhood 40°20'15"N 79°50'58"W approx. 2316, Riverview Avenue, Eden Park, McKeesport, Allegheny County, Pennsylvania, 15132, United States Precinct Margin: D+38%	Voter 940's Neighborhood 35°59'52"N 115°17'15"W approx. West Cactus Avenue, Clark County, Nevada, 89178, United States Precinct Margin: D+13%
Voter 941's Neighborhood 33°23'21"N 96°36'58"W approx. 2501, Hitching Post Trail, Anna, Collin County, Texas, 75409, United States Precinct Margin: R+24%	Voter 942's Neighborhood 38°35'28"N 121°18'0"W approx. 10486, Investment Circle, Rancho Cordova, Sacramento County, California, 95670, United States Precinct Margin: D+19%
Voter 943's Neighborhood 37°2'56"N 121°53'19"W approx. Aptos Creek Fire Road, Santa Cruz County, California, United States Precinct Margin: D+51%	Voter 944's Neighborhood 34°1'57"N 117°45'43"W approx. 93, Quiet Hollow Road, Pomona, Los Angeles County, California, 91766, United States Precinct Margin: D+28%
Voter 945's Neighborhood 44°57'58"N 93°17'12"W approx. Parsonage, Groveland Avenue, Loring Park, Minneapolis, Hennepin County, Minnesota, 554, United States Precinct Margin: D+79%	Voter 946's Neighborhood 30°26'58"N 91°5'16"W approx. 9114, Woodbine Street, Broadmoor, Castlewood, Baton Rouge, East Baton Rouge Parish, Louisiana, 70815, United States Precinct Margin: R+11%
Voter 947's Neighborhood 41°15'37"N 80°50'52"W approx. McGuffey PK-8, Tod Avenue Northwest, Hardscrabble, Warren, Trumbull County, Ohio, 44485, United States Precinct Margin: D+34%	Voter 948's Neighborhood 37°58'55"N 122°32'42"W approx. 143, Solano Street, San Rafael, Marin County, California, 94901, United States Precinct Margin: D+72%
Voter 949's Neighborhood 34°2'1"N 118°21'55"W approx. 2504, South Curson Avenue, West Adams, Los Angeles, Los Angeles County, California, 90016, United States Precinct Margin: D+79%	Voter 950's Neighborhood 33°34'37"N 82°11'53"W approx. Columbia Land Corporation Lake, Cumberland Court, Lake Cumberland West, Columbia County, Georgia, 30809, United States Precinct Margin: R+40%
Voter 951's Neighborhood 41°37'43"N 86°16'14"W approx. 440, West Ireland Road, South Bend, Saint Joseph County, Indiana, 46614, United States Precinct Margin: R+28%	Voter 952's Neighborhood 40°21'40"N 74°16'19"W approx. 222, Tennent Road, Marlboro Summit, Marlboro Township, Monmouth County, New Jersey, 07751, United States Precinct Margin: D+1%
Voter 953's Neighborhood 39°49'2"N 75°2'18"W approx. 50, Kelly Driver Road, Village of Glen Oaks, Gloucester Township, Camden County, New Jersey, 08021, United States Precinct Margin: D+20%	Voter 954's Neighborhood 36°25'59"N 81°26'6"W approx. 623, Ashe Central School Road, Ashe County, North Carolina, 28640, United States Precinct Margin: R+44%
Voter 955's Neighborhood 29°32'35"N 98°19'5"W approx. Kitty Hawk Middle School, 840, Old Cimarron Trail, Universal City, Bexar County, Texas, 78148, United States Precinct Margin: D+14%
Voter 956's Neighborhood 33°59'51"N 84°34'8"W approx. Noonday Church, Noonday Church Road, Marietta, Cobb County, Georgia, 30066, United States Precinct Margin: D+40%
Voter 957's Neighborhood 34°15'32"N 117°12'55"W approx. 26998, Golf Course Lane, Lake Arrowhead, San Bernardino County, California, 92352, United States Precinct Margin: R+18%
Voter 958's Neighborhood 33°54'51"N 118°19'13"W approx. 13001, Purche Avenue, Gardena, Los Angeles County, California, 90249, United States Precinct Margin: D+81%
Voter 959's Neighborhood 36°2'21"N 115°14'22"W approx. 6778, Cavatina Avenue, Enterprise, Clark County, Nevada, 89139, United States Precinct Margin: D+21%
Voter 960's Neighborhood 41°39'3"N 83°37'17"W approx. 3341, Inverness Avenue, Secor Gardens, Vulcan, Toledo, Lucas County, Ohio, 43607, United States Precinct Margin: D+88%
Voter 961's Neighborhood 44°4'30"N 123°5'48"W approx. 1199, Lorella Avenue, Eugene, Lane County, Oregon, 97401, United States Precinct Margin: D+44%
Voter 962's Neighborhood 42°59'39"N 85°55'25"W approx. 5349, Warner Street, Allendale, Allendale Charter Township, Ottawa County, Michigan, 49401, United States Precinct Margin: R+15%
Voter 963's Neighborhood 40°38'49"N 74°23'21"W approx. Forest Road Building, Forest Road, Fanwood, Union County, New Jersey, 07023, United States Precinct Margin: D+36%
Voter 964's Neighborhood 42°55'1"N 88°10'39"W approx. Stonecrest Road, Glen Oaks Estates, Muskego, Waukesha County, Wisconsin, 53150, United States Precinct Margin: R+41%
Voter 965's Neighborhood 39°16'4"N 76°51'10"W approx. 3799, Garand Road, Gray Rock, Howard County, Maryland, 21042, United States Precinct Margin: D+37%
Voter 966's Neighborhood 34°45'46"N 111°55'59"W approx. North Oak Creek Valley Road, Yavapai County, Arizona, 86325, United States Precinct Margin: R+16%
Voter 967's Neighborhood 42°7'39"N 85°56'40"W approx. 40910, 80th Avenue, Decatur Township, Van Buren County, Michigan, 49045, United States Precinct Margin: R+16%
Voter 968's Neighborhood 32°46'22"N 97°20'2"W approx. 1301, Poindexter Avenue, Fort Worth, Tarrant County, Texas, 76196, United States Precinct Margin: D+20%
Voter 969's Neighborhood 44°16'57"N 88°6'12"W approx. Greenleaf Road, Askeaton, Town of Holland, Brown County, Wisconsin, 54123, United States Precinct Margin: R+40%
Voter 970's Neighborhood 40°4'50"N 75°10'43"W approx. 8639, Temple Road, Ivy Hill, Philadelphia, Philadelphia County, Pennsylvania, 19150, United States Precinct Margin: D+93%
Voter 971's Neighborhood 40°11'5"N 82°53'40"W approx. 8158, Oxbow Road, Genoa Township, Delaware County, Ohio, 43082, United States Precinct Margin: R+24%
Voter 972's Neighborhood 29°35'12"N 98°29'31"W approx. 241, Limestone Creek, Hill Country Village, Bexar County, Texas, 78232, United States Precinct Margin: R+34%
Voter 973's Neighborhood 34°6'13"N 117°41'22"W approx. North Central Avenue, College Heights, Upland, San Bernardino County, California, 91786, United States Precinct Margin: D+42%
Voter 974's Neighborhood 40°16'22"N 74°31'39"W approx. 189, Park Avenue, Hightstown, Mercer County, New Jersey, 08520, United States Precinct Margin: D+39%
Voter 975's Neighborhood 41°43'26"N 71°18'48"W approx. 98, Bluff Road, Barrington, Bristol County, Rhode Island, 02806, United States Precinct Margin: D+47%
Voter 976's Neighborhood 39°19'10"N 89°32'22"W approx. 8207, North 22nd Avenue, Raymond, Montgomery County, Illinois, 62560, United States Precinct Margin: R+50%
Voter 977's Neighborhood 45°6'21"N 93°22'6"W approx. 6785, 83rd Place North, Brooklyn Park, Hennepin County, Minnesota, 55445, United States Precinct Margin: D+48%
Voter 978's Neighborhood 32°21'48"N 86°17'36"W approx. Alabama State University, 915, South Jackson Street, Montgomery, Montgomery County, Alabama, 36104, United States Precinct Margin: D+79%
Voter 979's Neighborhood 42°7'14"N 72°44'33"W approx. 32, George Street, Westfield, Hampden County, Massachusetts, 01085-3899, United States Precinct Margin: D+19%
Voter 980's Neighborhood 39°33'15"N 119°57'47"W approx. Hawk Meadow Trail, Verdi-Mogul, Washoe County, Nevada, 89523-3829, United States Precinct Margin: R+9%
Voter 981's Neighborhood 35°52'57"N 78°44'42"W approx. 3168, Glen Royal Road, Raleigh, Wake County, North Carolina, 27617, United States Precinct Margin: D+40%
Voter 982's Neighborhood 28°41'24"N 81°22'18"W approx. 1600, Orlando Avenue, Seminole County, Florida, 32750, United States Precinct Margin: R+6%
Voter 983's Neighborhood 40°43'55"N 73°51'41"W approx. 97th Street & 62nd Drive, 97th Street, Rego Park, Queens, City of New York, New York, 11374, United States Precinct Margin: D+3%
Voter 984's Neighborhood 44°16'30"N 70°30'11"W approx. 32, Richards Lane, Paris, Oxford County, Maine, 04281, United States Precinct Margin: R+7%
Voter 985's Neighborhood 45°1'56"N 87°11'49"W approx. 3435, Fairview Road, Town of Baileys Harbor, Door County, Wisconsin, 54202, United States Precinct Margin: D+19%
Voter 986's Neighborhood 37°9'42"N 76°30'57"W approx. 448, Waverly Place, Windsor Great Park, Newport News, Virginia, 23608, United States Precinct Margin: D+21%
Voter 987's Neighborhood 44°2'58"N 123°0'25"W approx. 1299, D Street, Springfield, Lane County, Oregon, 97477, United States Precinct Margin: D+20%
Voter 988's Neighborhood 35°19'41"N 119°3'42"W approx. 5448, Cherry Tree Lane, Bakersfield, Kern County, California, 93309, United States Precinct Margin: D+19%
Voter 989's Neighborhood 33°38'29"N 112°4'45"W approx. WinCo Foods, 330, West Bell Road, Central Park Village, Phoenix, Maricopa County, Arizona, 85023, United States Precinct Margin: D+0%
Voter 990's Neighborhood 39°30'39"N 75°40'47"W approx. Jamison Corner Road, New Castle County, Delaware, 19709, United States Precinct Margin: D+28%
Voter 991's Neighborhood 35°29'35"N 80°50'44"W approx. 577, Greenway Street, Downtown, Davidson, Mecklenburg County, North Carolina, 28036, United States Precinct Margin: D+35%
Voter 992's Neighborhood 40°19'40"N 75°19'36"W approx. 246, East Broad Street, Telford, Bucks County, Pennsylvania, 18969, United States Precinct Margin: R+4%
Voter 993's Neighborhood 33°50'21"N 84°21'14"W approx. 1019, Crane Road Northeast, Atlanta, Fulton County, Georgia, 30324, United States Precinct Margin: D+40%
Voter 994's Neighborhood 42°45'38"N 71°3'58"W approx. 263, Salem Street, South Groveland, Haverhill, Essex County, Massachusetts, 01835, United States Precinct Margin: D+13%
Voter 995's Neighborhood 37°20'38"N 108°35'51"W approx. Bravo! Cleaning & Restoration, 723, West 4th Street, Cortez, Montezuma County, Colorado, 81321-3299, United States Precinct Margin: R+14%
Voter 996's Neighborhood 27°17'56"N 80°20'40"W approx. 267, Southeast Ray Avenue, Port Saint Lucie, Saint Lucie County, Florida, 34983, United States Precinct Margin: R+2%
Voter 997's Neighborhood 40°35'13"N 73°40'6"W approx. 145, West Olive Street, City of Long Beach, Nassau County, New York, 11561, United States Precinct Margin: D+42%
Voter 998's Neighborhood 40°46'57"N 73°31'52"W approx. 20, 18th Street, Birchwood at Jericho, Hicksville, Town of Oyster Bay, Nassau County, New York, 11753, United States Precinct Margin: D+9%
Voter 999's Neighborhood 36°48'47"N 76°44'25"W approx. 47, Virginia Avenue, Windsor, Isle of Wight County, Virginia, 23487, United States Precinct Margin: R+36%
Voter 1000's Neighborhood 29°4'5"N 81°2'17"W approx. Port Orange Fire / Rescue Station 4, Airport Road, Sabal Creek, Port Orange, Volusia County, Florida, 32128, United States Precinct Margin: R+26%

---

Voting is Rational

17 Apr 2022

A common refrain in politics-adjacent discourse is “why bother voting? there’s no chance your individual vote will affect the outcome of the election!” This concept is often conceptualized in political science as the Paradox of Voting. However, with a few simple assumptions, the paradox disappears.

Yes, voting is unlikely to directly change the outcome,

Assume there’s v voters and the election is predicted to have a margin of \(x \pm y\) points. We can model the predicted margin as a normal distribution (usually a reasonable assumption) and then stretch this out by \(v\) to give a distribution of raw vote margins.

We then can use the height of this probability distribution at 0 (a tied vote) to roughly model the probability of a single voter swinging the election.

This turns out to be relatively easy to compute, and is given by the formula

\[h = \frac{1}{vy\sqrt{2\pi}} * \exp\left(-\frac 12 \left(\frac{x}{y}\right)^2\right)\]

This is often a very small value! For example, if you consider a typical election with 5 million voters in a close state, where the polling average is expected to be D+2, with a standard deviation polling error of 6 points, this ends up being 1 in 840,000!

So it’s easy to see why people think voting is irrational is irrational, as there is a very small chance you affect the result.

But the payoff to swinging an election is huge

However, it’s important to remember that if you’re deciding an election, you’re deciding the fate of every single person in the region of interest! This means that if you put a value of \(k\) on the average person’s quality of life improvement, and there’s n people in this society, the value of swinging an election is \(kn\). If we then express the number of voters in this society as \(v = nt\), where \(t\) is “turnout” (here defined as the percentage of people who vote), then we have that our formula becomes

\[h = k\frac{1}{ty\sqrt{2\pi}} * \exp\left(-\frac 12 \left(\frac{x}{y}\right)^2\right)\]

This lets us assign a dollar value to a marginal vote – that is to say, how much value should be assigned to persuading a single voter to vote before the election? Let’s take Georgia’s 2021 election, where Democrats campaigned on $1,400 checks for the populace (on average ~$700 per resident, as not all people got checks). In this case, with a predicted margin of D+1, the expected value of a marginal vote for the Democrats would actually be E = $9180 – each additional voter that they activate on top of the regular electorate would be worth $9180 to the state’s populace, based on the disbursement predicated on a Democratic victory. The below table highlights several other scenarios and how much a vote would be worth in each of those

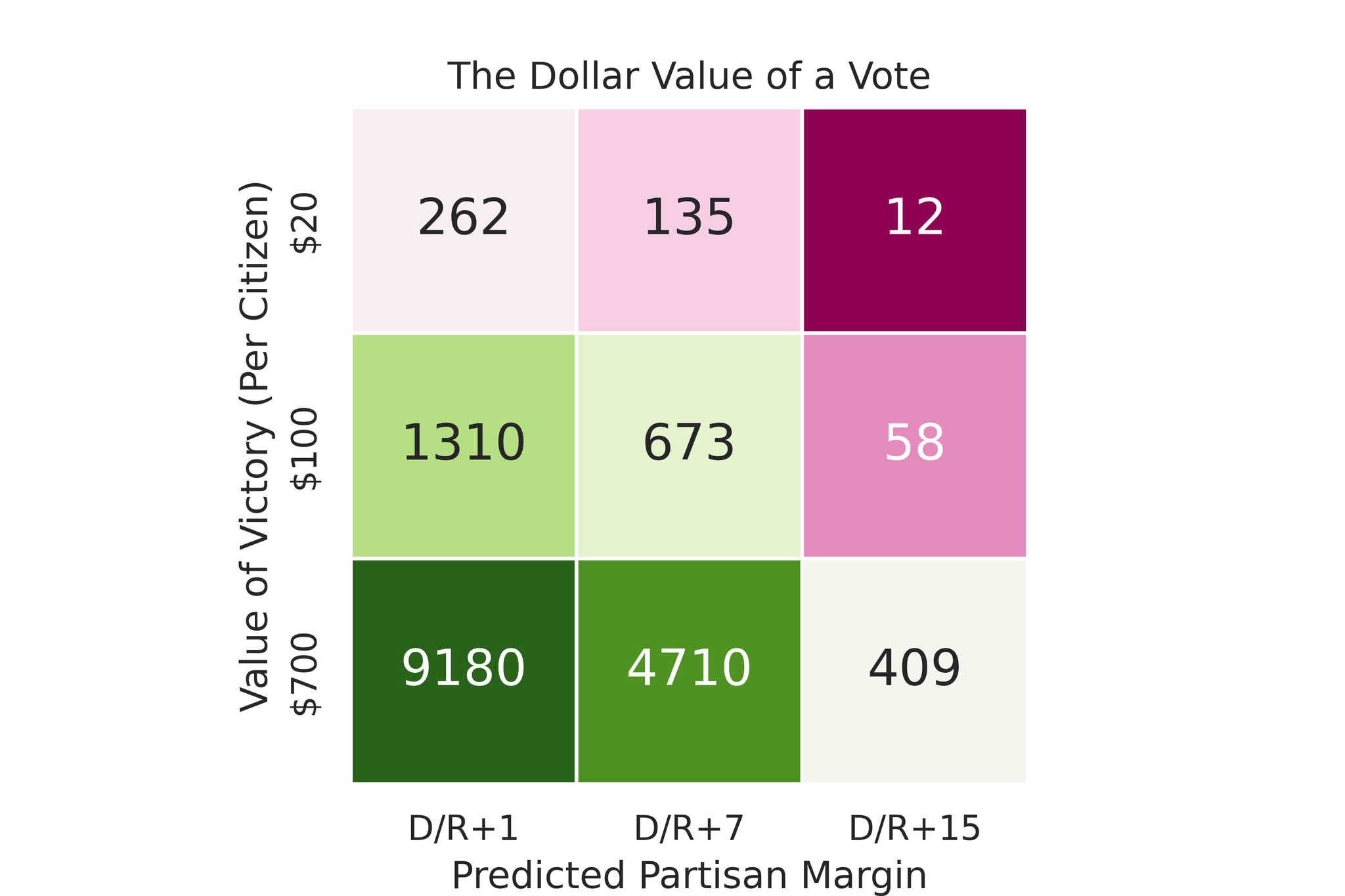
In other words, if voting is affordable and accessible, you should absolutely vote if you care about other people in society. Given how easy it generally is to vote (at most a few hours of time are spent), it is well worthwhile in almost all cases.

Caveats

The first caveat here is that we are assuming that a rational voter should care about other people in society. I think this is where the paradox of voting crowd would most take issue. However, we think it is reasonable to assert that a rational actor in a society should apply a universal perspective, otherwise more or less all forms of political action, from signing up to a union to following laws that are hard to enforce would be nullified.

Now of course, the value of a vote varies a lot depending on the circumstance. If, for example, you don’t have a competitive election (say, Tennessee, where the presidential outcome is predicted to be R+25), the value of a presidential vote is virtually zero, because your individual odds of changing the outcome are next to none, even once multiplied by the population. Here, the value of voting is probably not that useful, though in almost all cases, there’s other, closer elections on the ballot that are absolutely worth voting in. In short, voting is important!

---

You're calculating population density incorrectly

26 Sep 2021

The question “how do you calculate population density?” sounds like the kind of thing you’d see on a third grade pop quiz. Obviously, you would calculate it in the same way you would calculate any other type of density: you take the feature of interest and its population, and divide by area.

The issue is that this approach assumes that every part of the region of interest is equally valuable.

Why do we care about density?

For example, consider the following two islands:

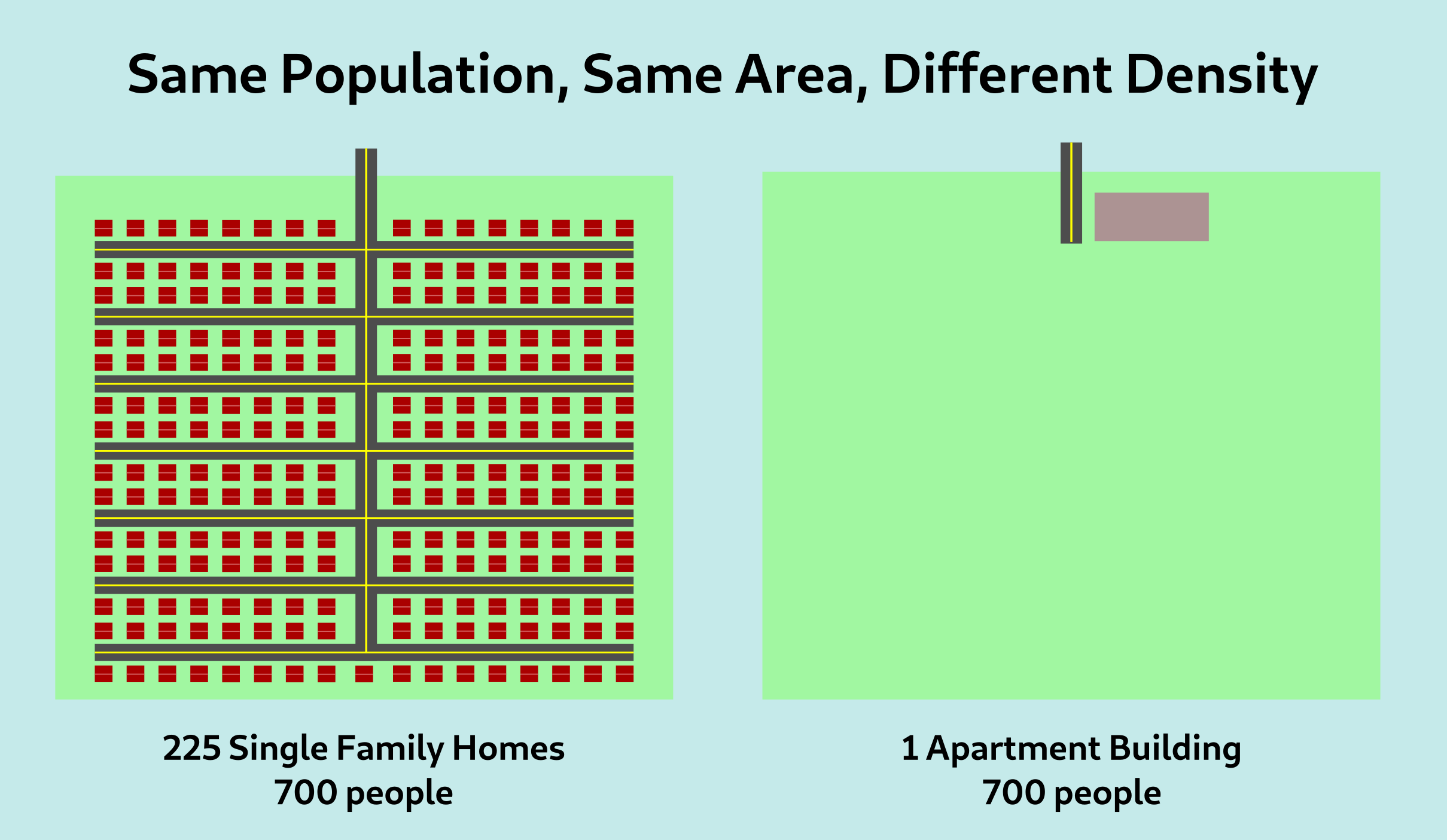
In both islands, the population is 700 people, and the areas are also identical. So by a standard population density metric, the two islands are the same “density”. This metric, however, misses something. The island on the right is far more dense than the one on the left, as perceived by the typical inhabitant of the island.

In practice, when we refer to density, we’re really referring to the density as experienced by people. Walkability, the viability of public transit, social trust, access to services nearby: all of these have to do with people and their interactions with other people. As such, a density metric that does not account for this will inevitably fail to capture that relevant context.

What is standard density measuring?

This seems like a strange question – obviously, it is measuring the mean number of people in every square meter of ground. However, another way to think about this is to divide our region up into smaller subregions; for example, let’s say each island is 1500m on a side and divide them into 9 regions each of 500m by 500m.

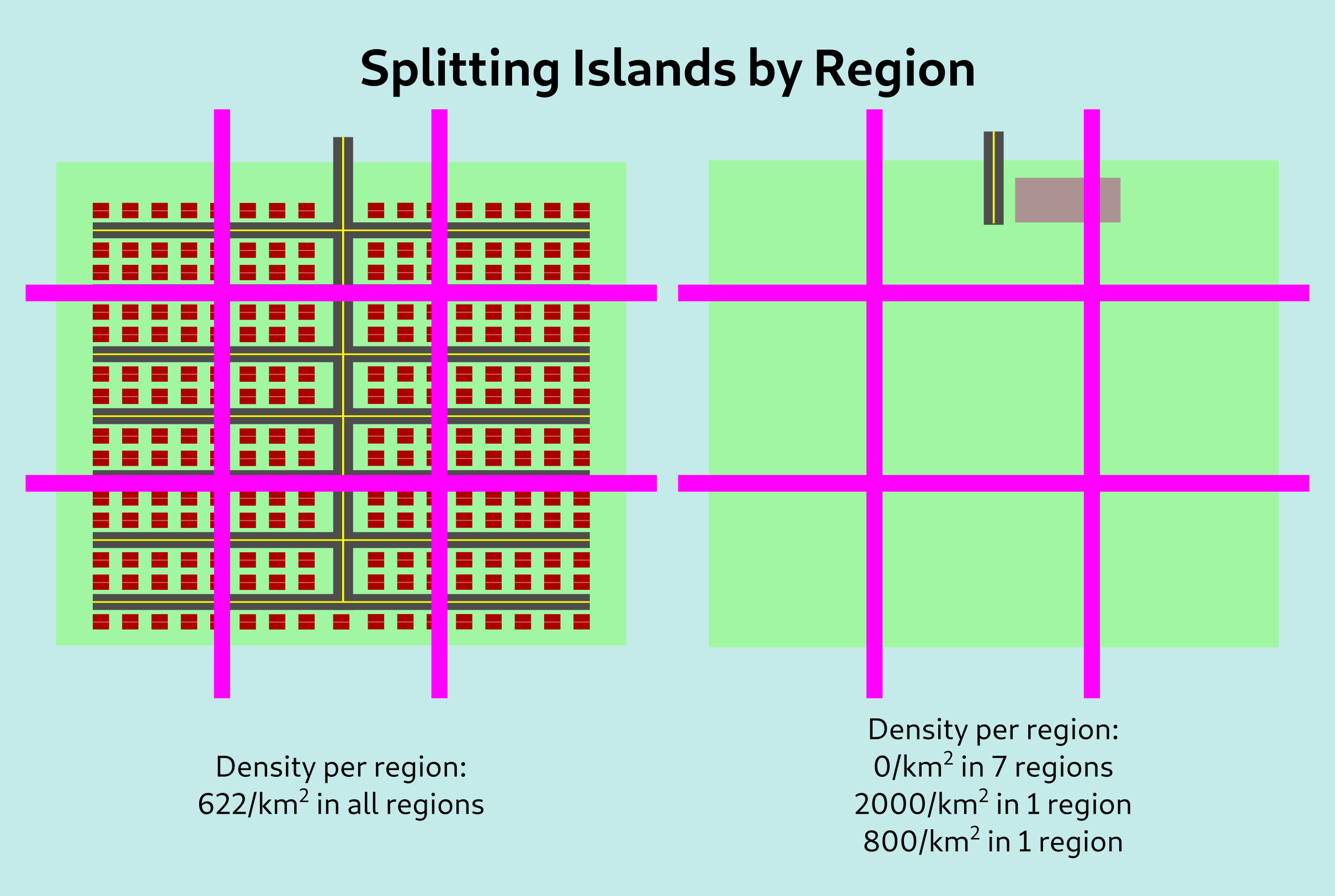
To calculate normal density, we would take the average of every region, weighted by its area, to get 622/km² in both of these cases. However, if we take the average of every region weighted by the population, we still get 622/km² for the left island but we get 1657/km² for the second island. This better reflects our intuition about the second island being more dense.

A practical metric

Of course, the issue with the above approach is the grid. If we had displaced the grid slightly to the right so the entire apartment building fell within it, we would have ended up with a density of 2800/km², and this kind of sensitivity to minor changes is really not what we want in a metric.

Instead of looking at a grid, we can instead look at disks of some radius, with one disk centered around each person. We compute the density in each disk, and then take the average of all these values across the region to compute the overall density.

Maps

And now for some maps! Depicted here are maps of the metric for radii of 250m, 1km, and 4km, based on 2020 census data.

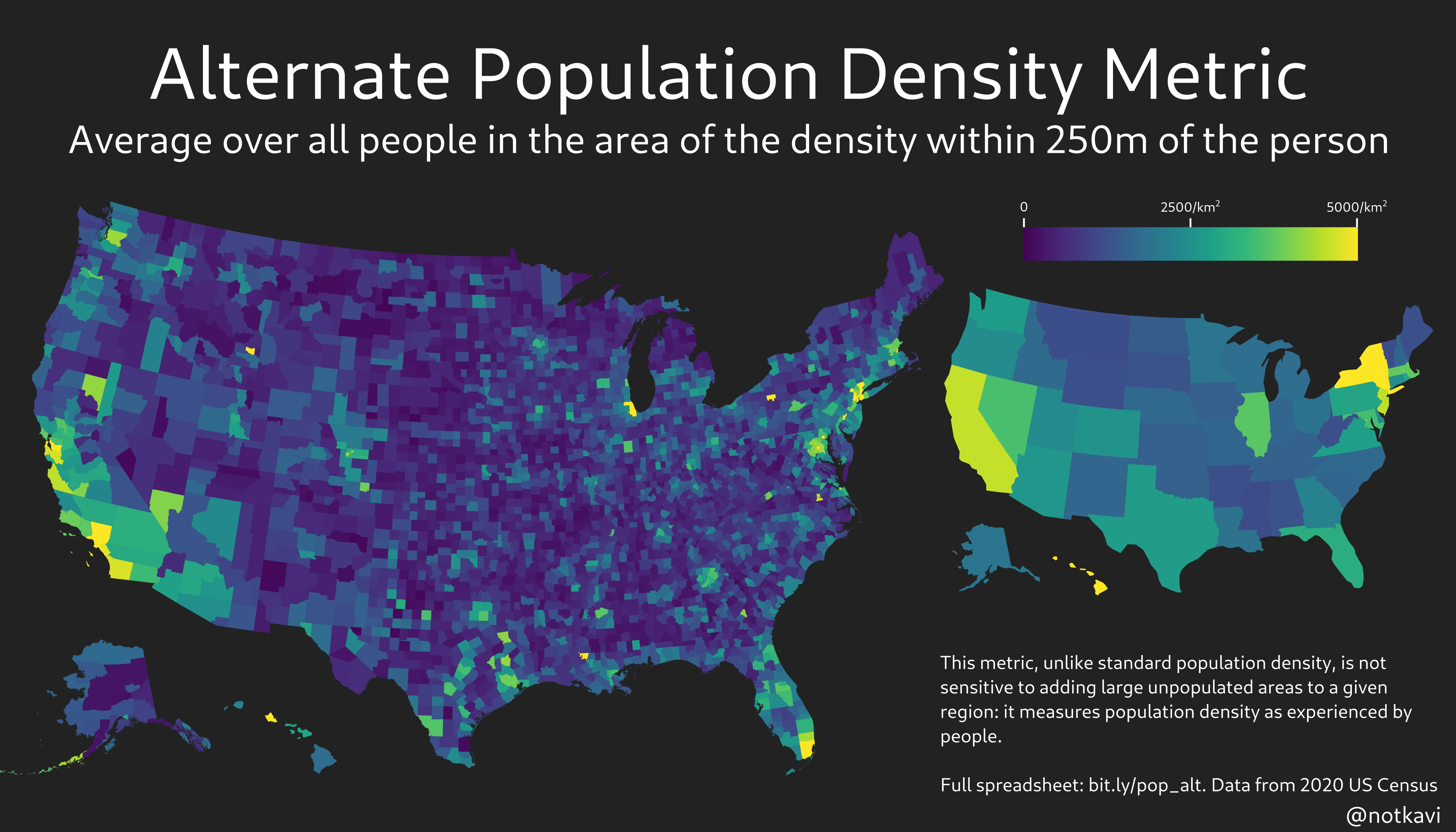
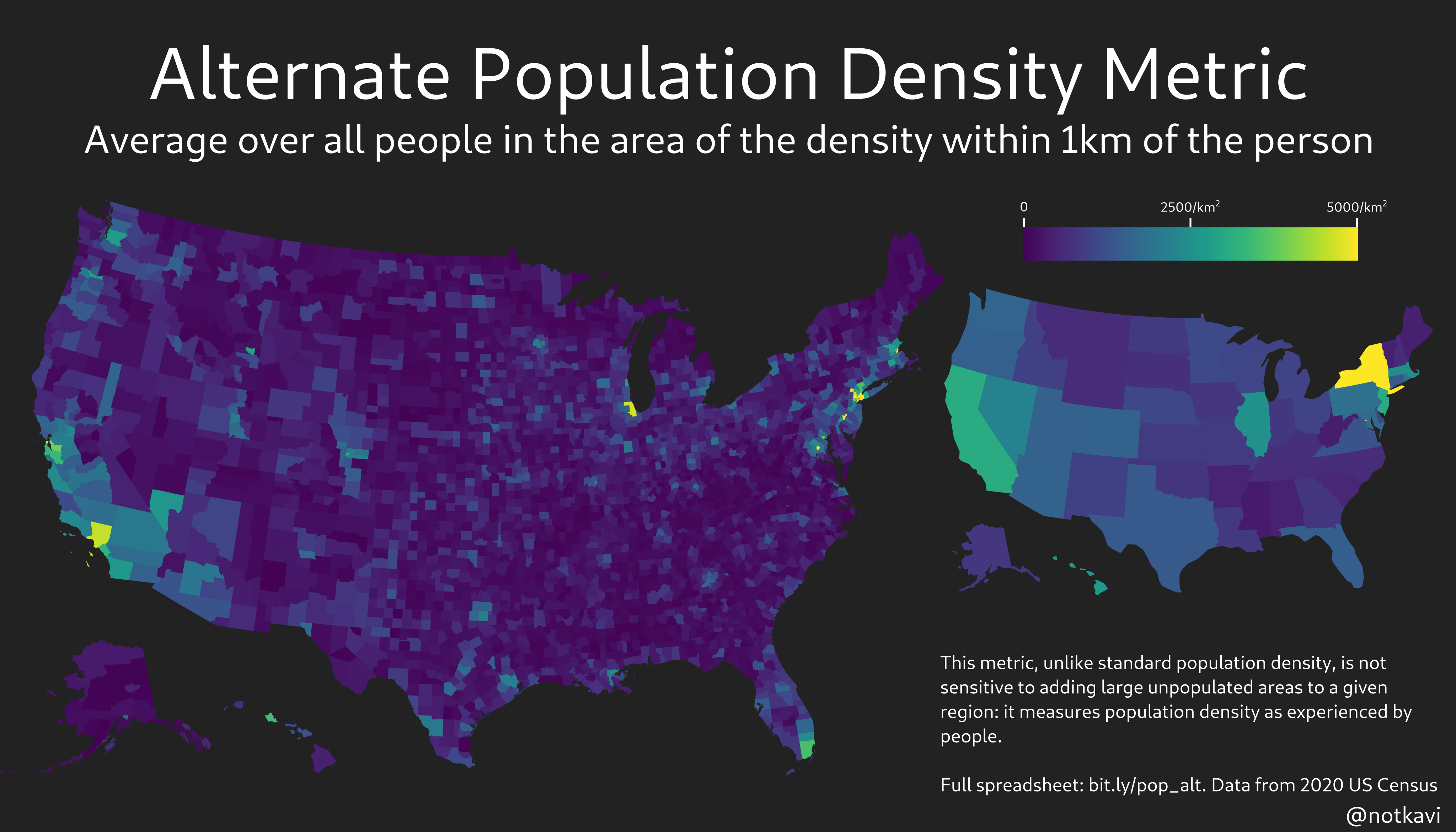
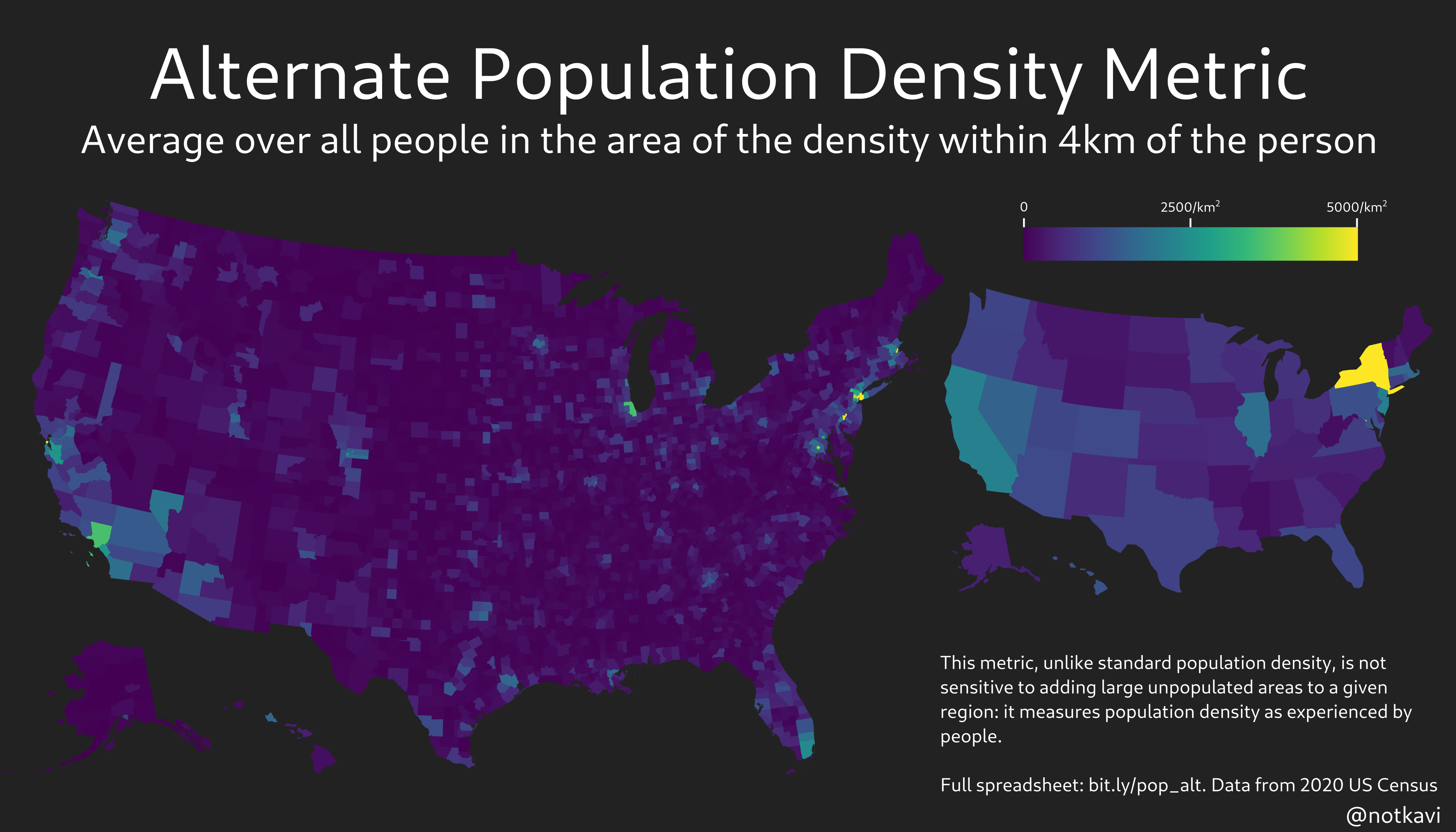
Note that New York State is easily the densest state by any of these metrics, which makes sense since most people in New York State live in very urban areas!

Political analysis

We all know that density predicts electoral outcomes right? Well, here’s what density vs Biden’s share looks like using several different metrics, by county.

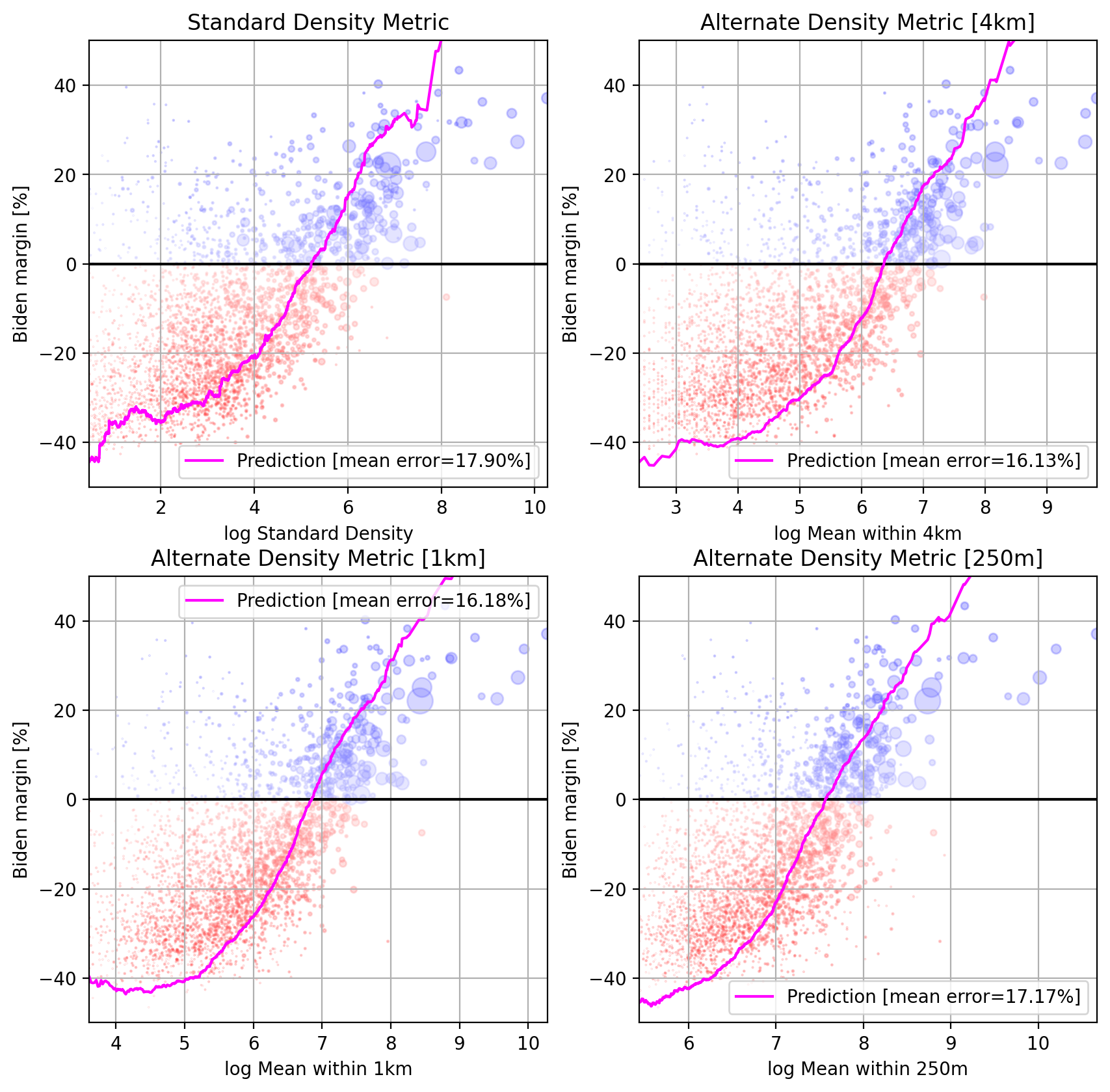
Note that the mean error is lower for the alternate density metric, but by 250m, it starts rising again. This is probably due to the fact that the census data used to construct this is block level, so noise from the exact placement of the blocks starts becoming relevant below 1km or so.

We can also map out the predictions and see what’s going on:

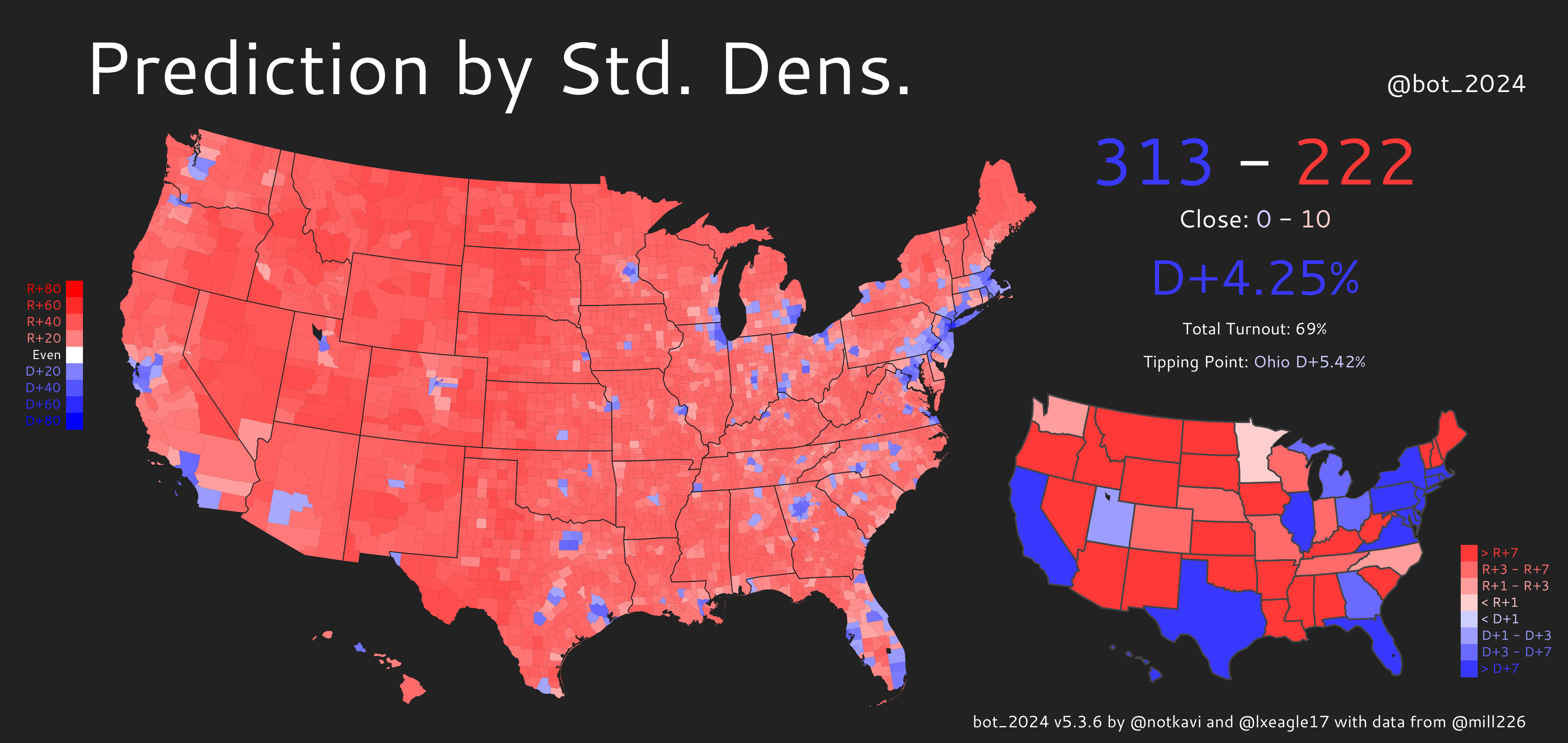
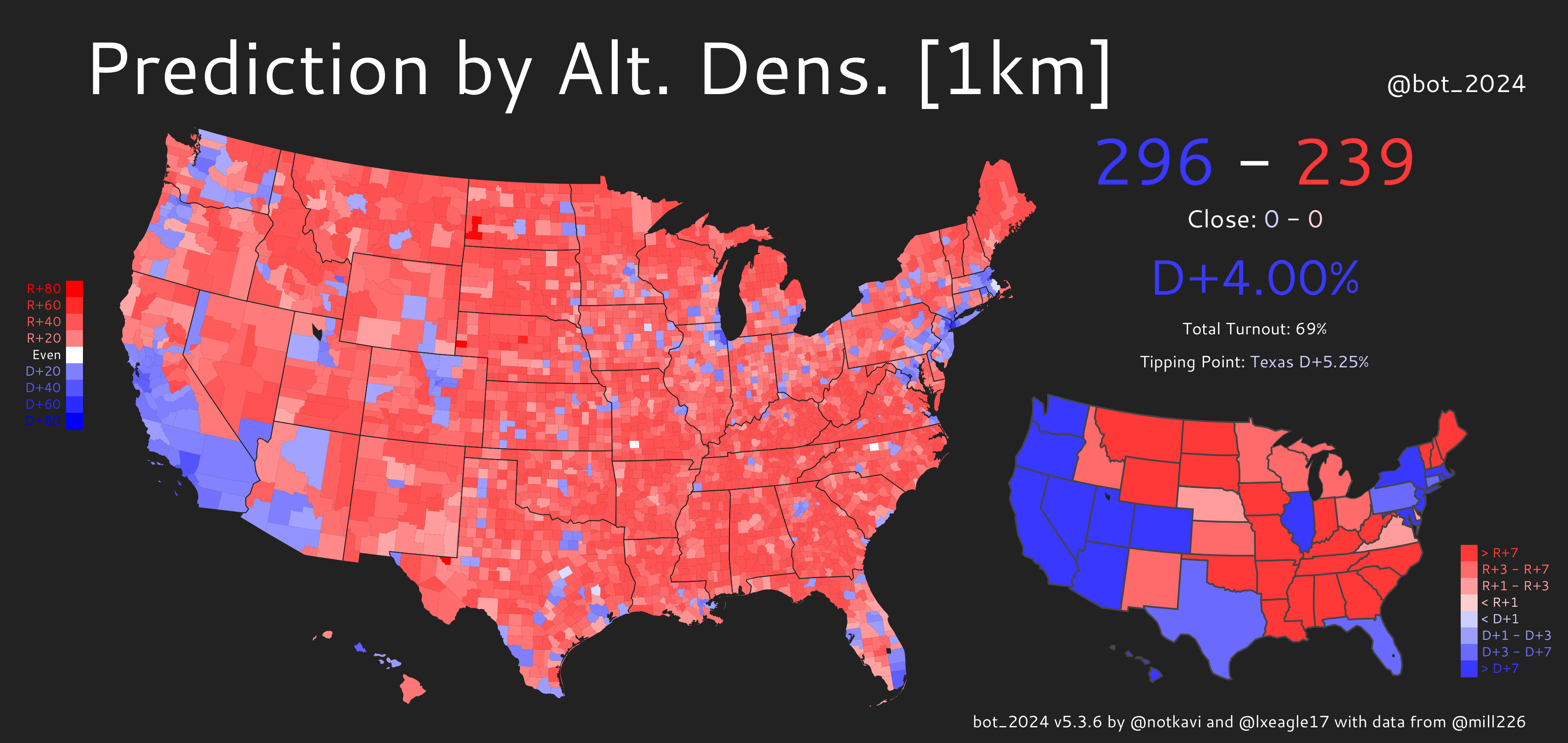
You can see that there’s far fewer blue counties by either of these metrics than Biden actually received, but the alternate density metric produces a better map as it can identify large counties that are nonetheless densely populated, especially in the Western US, where counties tend to be much larger.

We can also see this on the residual maps:

Both maps show obvious patterns where the Great Plains, Appalachia, Utah, and Florida are redder than expected by density, while Native, Hispanic, Black, and secular areas, along with the midwestern Driftless area, are bluer than expected. However, you can see that standard density has an additional pattern where pretty much the entire west is much bluer than expected. This is because the west tends to have large counties such as San Bernardino and Riverside counties (California), Clark County (Nevada), or Maricopa County (Arizona) that are large in area, but are not actually nearly as sparse as the standard density metric would suggest.

One interesting sidenote: in both predictions, the tipping point state’s margin is more Democratic than the popular vote margin. This means that in a neutral, D/R+0 political environment, the Democrats would win!

Consequently, we can see that when only accounting for urban areas being more Democratic, the EC/PV gap would favor Democrats, unlike our current political reality, in which it favors Republicans. One direct implication of this is that the Electoral College actually favors urban areas over rural ones!

Conclusion

Anyways, I hope you enjoy and have something to think about when it comes to calculating density! You can view and download the values by county here. Please let me know if you have any comments, you can reach me at @notkavi on twitter. Thanks to @lxeagle17 for helping with editing, I lack basic grammar skills.

---

BAN ALL AMBIGUOUS MATHEMATICAL EXPRESSIONS

07 Aug 2021

If you’re on twitter or Facebook you’ve probably seen this expression (or a variant with different numbers) before

The question that goes with it is “can you solve this?” and there’s usually a massive debate among people in the comments about whether the answer is 9 (corresponding to dividing first then multiplying by (1+2)) or 1 (corresponding to multiplying first to get 6 then dividing).

Order of Operations

One thing people often seem to be arguing about is PEMDAS/BODMAS: the system of precedence used to do these operations. The acronyms suggest a sequencing of multiplication and division, but the convention taught with them is that the two operations have equal precedence and should be left associatively evaluated. So the formula would parse as (6 ÷ 2)(1+2) and thus be equal to 9.

One common response to this from mathematicians and other more sophisticated observers is that people are arguing about a completely arbitrary convention, and really you should just parenthesize better. These folks are correct, but I think they’re missing something that makes this particular example unique. For example, I think most people would correctly recall and apply the PEMDAS rule to the formula

I think most people would even correctly apply the rule to the formula

There’s something unique about this formula that means that PEMDAS does not apply to it.

The implicit multiplication operator

If you saw the following equation, how would you parenthesize it?

I think most people would correctly parenthesize this as T = (PV)/(nR) not T = P(V/n)R.

Most folks would say you should probably still parenthesize to be sure, but many people would casually just write PV / nR and be understood by 100% of their target audience. In a textbook you’d write \(\frac{PV}{nR}\) and that’s how the mind reads it.

There’s even some cases where a textbook would actually use the / operator!

If you’ve taken an abstract algebra class, you’ve seen a function type written as something like

Ignoring the arrow and colon (which have lower precedence than everything else), we have the type

which represents a pair of integers modulo 2. The correct parenthesization of this type is thus

Note that we don’t actually use the standard left-to-right PEMDAS rule here, nor do we prioritize multiplication over division. Instead, we have the following precedence: implicit multiplication, / division, then × multiplication.

The division bar

Ok so we’ve established that the precedence rule for division and implicit multiplication is such that implicit multiplication works differently from × multiplication. We’ve also kinda justified that the answer should really be 1 by standard conventions in higher math

The thing is that the division bar is a really weird object – it isn’t actually used much outside of elementary school mathematics. Typically outside that context either a full division bar \(\frac 2 3\) or an inline division bar /. That means that in practice there’s no actual convention about the relationship between ÷ and the implicit multiplication operator.

Conclusion / TLDR

The expression 6 ÷ 2(1+2) is probably the most controversial mathematical expression out there. It is capable of being interpreted differently even among people who definitely understand the standard conventions of mathematical symbology intuitively and fluently.

It is not just a normal level of unnecessarily confusing, it is adversarial in it’s confusingness.

STOP POSTING IT. BLOCK ALL WHO POST IT. DISENGAGE WITH DISCOURSE SURROUNDING IT.

---

Setting the actual size of figures in matplotlib.pyplot

18 May 2019

Let’s say you want to set the size of a figure in matplotlib, say because you want the captions to match the font size on a poster (this came up for me recently). However, you might find yourself with kinda a weird problem.

Directly setting the size of a figure

Setting the actual size of figures in matplotlib.pyplot is difficult. Setting the size of a figure as so

It’s the right size in pixels, except that this image is padded weirdly and the x label is cut off (border added).

Tight Layout

The fix for this is to use a tight layout in the output

This fixes the elements being dropped issue, but the image size is now incorrect (at 2.59x4.62 instead of 2.5x5).

Fixing the problem

First, we write a general function to get the size of a figure. We then calculate \(x_{\text{to set}} = x_{\text{set previously}} \frac{x_{\text{target}}}{x_{\text{actual}}}\) for \(x\) being the width and height. The intuition behind this equation is that we figure out how off the actual image’s size is from our target, and use this to update what we tell matplotlib to do.

However, this is an approximation, and we repeat it to get a better fit. The full code is below:

Using this method (note that we no longer need to set the figure size when creating the figure)

we get the following result, which is exactly the correct size.

What’s with the return False?

The reason that we check to see if the error is increasing is that sometimes it is impossible to fit a plot within a given space. For example, take the following example

This ends up trying to decrease the height of the figure to below 0, but before it can cause a crash in matplotlib, it causes the last condition in set_size to be activated, leading to a False return value. The resulting image is 91x109, nowhere close to the 100x50 that it should be, and looks like this

By returning False, this allows e.g., a notebook to finish executing in cases where it is unecessary to check, but a simple assert set_size(fig, (1, 0.5)) would lead to an error if that is desired.

Conclusion

The example above is full, working, code, and should honestly probably be part of matplotlib: generally speaking, when I set the size of a figure, I intend to set the actual size of the figure, not the size of the plot with some minimal padding around it. In any case, hopefully this code is helpful to you!

---

Understanding Python's interactive mode

18 Oct 2018

The Python interepreter has this convenient feature that when you type something simple onto the interpreter, it spits that value back out at you, so you can copy/paste it back as a value.

But with convenience often comes complexity, let’s look at how this feature works!

How does the print function work?

Before we can talk about typing stuff onto the interpreter, let’s talk about the simpler function print. Let’s take a look at a few examples:

So how does print work? Clearly, it returns None once it’s done. But what’s it doing when it’s printing to the screen. Clearly, something strange is happening where both the string '1' and the number 1 get printed out as the single character 1.

To properly understand print, we need to break it down into its constituent parts. Imagine we have a function print_string, which takes a string and prints it to a terminal. Then, we have the following behavior:

Which is somewhat more consistent. We can implement print_string in terms of print fairly easily as follows:

where str is a function that takes in a value and outputs some string. We have the following behavior for str (illustrated using lists for reasons that will become clear later).

In the case of a string, it does nothing, and in the case of an integer, it converts it into a string. We’ll come back to str later, but for now think of it as providing a nice human-readable version of the given object.

repr

But if we want an output that isn’t human-readable, but is instead computer-readable, we can use repr instead. For example, repr(1) and repr('1') should produce different outputs as they should be read as two different types. Let’s look at some examples:

Note for later: print_string(repr(<blah>)) prints out <blah>

Looking at an the same example as before using an environment diagram, we have the same result for repr(12) as str(12) but repr('12') has a set of quotes around it while str('12') does not.

This difference can be attributed to the fact that typing in 12 gets us 12, while we need to type in '12' to get '12', whereas 12 appropriately represents both concepts to a human reader.

Typing something into the interpreter

In the last section, we saw how the repr function works, especially on strings, where it adds a layer of quotes. You might notice that typing something directly onto the interpreter performs a similar task. That’s because it more or less is. We can consider typing something directly into the interpreter (>>> x) to be the same as calling >>> print_string(repr(x)). The examples from above have the same behavior:

In fact, this is the motivation behind repr, if you type something into the interpreter, it spits it back out at you.

Typing repr(something) into the interpeter

Let’s say you did the following:

What happened? We now have two sets of quotes around the hi. Did the repr function add two sets of quotes instead of one? The answer is no, because, as you can recall from the previous section, that example is equivalent to

Using our environment diagram, we can see the following:

We see that repr('hi') has four characters in it: ', h, i, and '. repr(repr('hi')) needs to represent this, so it has six characters in it: ", ', h, i, ', ". These six characters get printed to the terminal, to form the string "'hi'".

__str__ and __repr__

OK, so now that we know that str, repr, print, and typing something directly into the terminal do, let’s look at how these concepts apply to user-defined functions. Take the following class:

The idea is that whenever we call str(x) when x is of type A, this is equivalent to calling x.__str__(), and whenever we call repr(x) when x is of type A, this is equivalent to calling x.__repr__().

Examples

Here are some examples of how custom __str__ and __repr__ methods work in practice. Before we get into the explanations, try to figure them out on your own

Your first question might be: why no parentheses when we type a into the terminal? The answer is that >>> a is equivalent to print_string(repr(a)), and we have that repr(a) is the string of length 2 containing the letters h, and i; which then gets printed. On the other hand, >>> repr(a) is equivalent to print_string(repr(repr(a))), and repr(repr(a)) is the string of length 4 containing the letters ', h, i, and '. The following environment diagram describes how this process happens:

---

Simulationism: Beyond the Matrix

14 Oct 2018

Simulationism is a fairly popular concept. There are many who subscribe to it: from those who use it as a thought experiment to argue against undisprovable theories to those who actually believe we are in a simulation since almost all universes should be simulations. Despite the disparate uses for simulationism, it is generally viewed as a fairly banal concept: the universe is a simulation, and that means absolutely nothing, practically speaking.

However, lurking beneath the seeming simplicity of the idea lies a far more radical set of implications.

Pure simulationism vs the Matrix

Simulationism is often explained as such: “we’re all living in a simulation, like the Matrix.” For most purposes, this is a good working definition. Mostly, I’ve seen simulationism used as kind of the ultimate Russell’s Teapot: an entirely undisprovable concept. As a Teapot, simulationism is a useful concept because it posits an alternate picture of the world that has no observable differences from ours: this property is true of the Matrix as well (well, apart from the glitches, and the actual plot of the movie).

On the other hand, there’s an important difference between simulationism and the Matrix. In the Matrix, when you wake up, you are you: a real human conciousness produced by a meat brain whose sensory inputs are being manipulated to place you into an alternate reality. However, in simulationism, you can’t wake up, because there is no underlying you: your entire existence, conciousness and sensory experience alike are the interaction between bits of information held in computer memory.

All is information

This difference is fundamental: simulationism presupposes a philosophical concept that the Matrix does not: all that reality is can be reduced to information. This isn’t quite materialism (in fact, it’s listed as one of the criticisms of materialism on materialism’s Wikipedia article¹) but it is similar in its reductionist approach. To many, this seems like a pedantic point: this assumption is an easy one to make (unless you believe in a soul or other such concepts).

What is a simulation?

So let’s say our universe is indistinguishable from a simulation. What is a simulation? Well, in a conventional sense, a simulation is a program running on data. The program is some set of instructions that allows us to go from one state to another. Take the following very simple world which exists in one of two states: 0 or 1. There are only two possible sets of laws for this universe: the laws that keep it steady or the laws that cause it to flip back and forth. What about 1, 1, 0, 1, 1, 0, ..., you might ask? Well, in that case the first and second 1s are different, which means that there is some additional state that the universe isn’t taking into account.²

For even more complicated universes, we’d want to be able to write down some mathematical formula or algorithm so we could actually run a simulation. It turns out that this isn’t always possible for infinite universes (since the laws might take infinite space to write), but let’s assume the universe is very large but not infinite and thus the rules can be written down.

Now some of you complexity fans out there might be thinking “wait, wait, wait, every set of laws of the universe might be expressible but only some of them would be quickly computable on a concise representation of the universe’s state”. Well, that’s true. But also, does it really matter how slow the simulation runs?³ The concept of time is a product of the laws of the universe: it really shouldn’t matter how long a second inside the universe takes outside the universe.

Is any running computer a universe?

One of the more interesting things about simulationism is that it allows us to imagine ourselves creating a universe. If we created a powerful enough computer and figured out close enough approximations to the laws and initial state of our own universe, we could set up our own simulation of a universe similar to ours.

But let’s say we didn’t bother with any of that. Let’s say we created a significantly simpler universe than our own on hardware we have sitting on our desk anyway. Is that simulation itself a universe? More generally, any running computer with no input or output from the outside world is a simulation of something, right? It has some state and rules for how to get from one state to another, which was our only definition of a universe.

Is any running computer a universe? Well, we seem to be backed into a corner: the answer has to be yes. One consoling fact is that the universe created by a computer running a screensaver would be nothing like our universe, it would be so dissimilar as to even make such a comparison quite a stretch.

Do we need the computer?

Let’s say I tell you about a simulation I have in mind: say the state is a number from 0 to 10 (starting at 1) and the law of the universe can be described as the function \[f(n) = 2n \mod 11 \] You could write a program to simulate this universe: you’d get a cycle of length 10 that went through every state but 0. But that cycle was fixed before you started running the program. Isn’t the mere existence of the program then enough to set up the universe? More concretely, the function \[g(n) = 2n \mod 4384165182867240584805930970951575013697 \] (credit to UTM for the prime) has more or less the same behavior, though a much longer cycle, which we know even without running the simulation (which would take \(5000\) times longer than the age of the universe to compute on my desk computer). Does running the simulation even matter if writing it down plans its entire history out anyway?⁴

So now, a program to calculate the next state, and a first state, written down together comprise a universe.

Do we need to write it down?

But now we’re in a weird spot: do we need to write the rules of the universe down? I’m not sure what the magic is of writing anything down, really. It’s strange to imagine that a simulation of our universe begins to exist the moment we write it down. The mathematical object that is the universe certainly does not begin to exist: and at this point, what’s the difference between the universe and its representation?

Of course, we’ve gotten to a truly ridiculous point: what this implies is that our universe could be a simulation, not running in some containing universe’s computer, not written down on the page of some containing universe’s book, but simply because it is mathematically possible. Similarly, every other universe with a slight modification of the laws of physics also exists in some other universe. Even more strangely, the universe identical to ours except that on January 1st, 2019, all blue objects turn green exists.⁵

If we’re in a simulation, then all things are happening

Simulationism, with a few additional assumptions I’ve made along the way, leads inevitably to a really strong version of multiple universe theory: anything that can be mathematically described exists in some real world. More relevant to our current universe, if every possible set of laws is happening, we don’t know that our universe has parsimonious laws. That means that we are equally likely to be in the “all laws normal” universe as we are to be in the “all blue objects turn green” universe. Thus, allowing for the premise of simulationism implies that scientific induction is literally impossible. The universe looks like it has laws simply by chance, and that fact could change at any minute.

One reason I think a lot of people are relatively comfortable with simulationism is because it seems relatively limited in its implications. In its simplest form, it’s a creator allegory, with the simulation’s programmers taking the place of a more conventional god figure. If thought through to its conclusion, it really is a far more radical idea, with jarring results.

---

Lists and Nonlocal in Python

03 Oct 2018

Mutable closures

A closure is a function with a parent frame that contains some data. If the parent frame can be modified, the function is said to be mutable.

For example, take the following doctest:

The c is called multiple times and returns a different value every time; but its state isn’t global as there is the d function which also counts up but on its own tineline.

The Python programming language allows for the creation of mutable closures in two different ways: one that is traditionally considered “functional” and one that is traditionally considered “object-oriented”. Let’s take a look at them now:

Nonlocal: Functional mutable closures

The most obvious way to implement the make_counter function is as follows:

The line nonlocal current_value ensures that the current_value variable assigned in the c frame refers to the value from the parent frame. Thus we have shared state (the current_value variable) which can be modified, the necessary components of a closure.

Lists: Object-oriented mutable closures

But do we really need anything that complicated? What if we did this?

Every time we call the resulting function, we get 0, 1, 2, 3, 4, 5, and then 6. This isn’t quite right, as it doesn’t go on forever, but it’s definitely a mutable function, and we never used nonlocal. What’s going on here? Let’s unroll the function somewhat:

Here we have that we can modify lst from the parent frame without assigning to it, since the contents of lst rather than the variable itself is mutated. We can exactly duplicate the original make_counter function as such:

Now, this looks like there’s an assignment to current_value on the commented line, but in fact, current_value[0] += 1 is equivalent to current_value[0] = current_value[0].__iadd__(1), which is equivalent (for numbers) to current_value[0] = current_value[0] + 1, and that is equivalent to current_value.__setitem__(0, current_value[0] + 1), which is not in fact an assignment.

Complications: Nonlocal on lists

Let’s say we write a few alternatives for make_counter:

Interestingly, the first two work but the last does not. Why? Aren’t a += b and a.extend(b) equivalent? Actually, they’re almost equivalent. a += b is equivalent to a = a.__iadd__(b), where __iadd__ is a special function that you can choose to implement on your class. In the case of Python, list.__iadd__ is equivalent to list.extend except that it returns a reference back to the same list.

Therefore, if you want to use a += b where a is a list, you thus need either to make a nonlocal or use a.extend(b) instead.

---

Confirming that timezones exist with minimal trust

27 May 2018

I was listening to an episode of Oh No, Ross and Carrie! about Flat Earth and it struck me that if you believe the world is conspiring against you, it’s practically quite difficult to prove almost anything. Now one thing that most Flat Earthers do seem to accept is that when its day in one part of the planet, it’s night in another part.

However, let’s say someone denied this. How would you prove it, with the minimum amount of trust?

Can we do this while trusting nobody?

Let’s say that our experimenter only trusts their own senses. Can they prove that the day/night dichotomy exists? Well, one way they could do this would be to confirm that their watch is correct, then fly to the other side of the world, then confirm that their watch was off by 12 hours from the day/night cycle. However, this isn’t exactly right, it’s possible that someone could mess with your watch to cause it to run slightly fast or slow and cause it to be different when you alived as when you left.

With a fast enough plane, you might be able to confirm that day had turned to night in less than 12 hours, without the need to rely on a possibly manipulable watch. However, the very act of stepping on a plane might allow nefarious agents to manipulate your subjective experience of time, thus fooling you into thinking time zones exist. (Yes, this is a massively unproductive view of the world, but let’s try to work around it.)

Given these limitations, it’s clear that our prover needs a collaborator they can trust.

Basic protocol with a trusted collaborator

We now have two experimenters, who each trust each other and want to prove the existence of time zones: Alice and Bob. Consider the following protocol: Bob travels across the world while Alice stays behind. Alice and Bob then communicate with each other and confirm that one sees day and the other night.

This works right? Well, almost. The issue is that there’s no protection against a simulation attack: what if Alice speaks to a simulated version of Bob while Bob speaks to a simulated version of Alice, with the two conversations actually taking place 12 hours apart from each other?

Alice and Bob’s position is starting to look undisprovable. But is it?

Shared Password

Let’s say that before leaving, Alice and Bob come up with a shared password, \(p\), randomly. Then, the protocol is as such:

• Alice and Bob: agree on password \(p\)
• Alice: goes to other side of the world and confirms that its day
• Alice: sends \(p\) to Bob
• Bob: confirms that its night and that the received message is in fact \(p\)

But wait, the adversary could trap the password after Alice has sent it but before Bob has received it, thus delaying it 12 hours and allowing the protocol to go through, even if the world in fact has no time zones. The issue is that there’s no response from Bob. Bob just sending back the password doesn’t help, since the adversary could do that!

Different Passwords

OK, so now we have two different passwords \(p_a\) and \(p_b\). The protocol is now as follows:

• Alice and Bob: create passwords \(p_a\), \(p_b\) and share them with each other
• Alice: goes to other side of world and confirms that its day
• Alice: sends \(p_a\) to Bob
• Bob: confirms that its night and that the received message is \(p_a\)
• Bob: sends \(p_b\) to Alice
• Alice: confirms that it is still the same day and the received message is \(p_a\)

Now, Alice knows for sure that the world in fact has multiple time zones.

However, Alice and Bob might say that the adversary has the ability to read and edit their memories and thus steal their passwords. OK, this objection must make their claim undisprovable, right? In this case the answer is yes, because the adversary could always just convince them that the world had timezones by making arbitrary modifications to their memories.

However, if we give the adversary only read access to their memories, their position turns out not to be undisprovable!

Secure Time Synchronization

The issue that Alice and Bob are running into is that they can’t pre-agree on the passwords, because then they know the passwords ahead of time and thus the adversary knows the passwords ahead of time. However, they might be able to “post-agree” on the passwords, as such:

• Alice and Bob: start on opposite sides of the world
• Alice: Confirms that its day
• Alice: Generates and sends \(p_a\) to Bob
• Bob: Confirms that its night
• Bob: Generates and sends \(p_b\) to Alice
• Alice: Confirms that it is still the same day
• Alice: meets with Bob
• Alice and Bob: check that all passwords transmitted were correct

If this protocol goes through without Alice and Bob having any issues, then they know that it can be day and night at the same time in different parts of the world. The procedure works!

Assumptions and Proof

OK, so if we wanted to prove that the above scheme works, we would need a few assumptions. First, we assume Alice and Bob are trustworthy. Second, we need to assume that Alice can confirm that some entity is Bob in a face-to-face conversation and vice versa (so that the Alice and Bob at the end are guaranteed to be the real Alice and Bob). Third, we need to assume that Alice and Bob can tell when night falls, that is, the adversary can’t somehow convince them that two points in time are on the same day when it was in fact night in between those points. Finally, the adversary cannot have time travel and cannot predict either Alice or Bob’s random number generators.

In this case, we can prove that Bob confirming that it is night where he is happened after Alice generated \(p_a\) and thus during some day D where Alice was, and before Bob generated and thus before Alice received \(p_b\) and thus before some point on the same day D. Since we assume days are continuous, this proves that Bob observed night during a time when Alice observed day, and thus this procedure is secure.

You can weaken the assumption that two specific trustworthy people are needed by repeating this procedure for every pair of people in some set of N people. Then the scheme proves that time zones exist assuming that 2/N of the people are trustworthy, at the cost of having to repeat the scheme \(O(N^2)\) times

Implications

N/A.

Less facetiously, I guess my general takeaway is that “your claim is undisprovable” shouldn’t be used as a synonym for “you’re making ridiculous, conspiratorial, assumptions”. Because even when someone is being paranoid, there might be a way to disprove their hypothesis, with enough effort.

---

Infix Notation in Scheme

11 Apr 2018

Scheme is well known as a very simple programming language. The general concept behind scheme is that it is composed of S-expressions, or expressions of the form (operator operand1 operand2 ... operandn), which can be nested.

This makes scheme relatively simple to parse and evaluate, however it does lead to some strange compromises on the style of programming. For example, rather than writing 12 * (2 + 3), you have to write (* 12 (+ 2 3)). And in a way, this is elegant in its simplicity.

But simplicity is overrated.

Homoiconicity, or writing a scheme program to write a scheme program

Scheme has this cool property of being a homoiconic language. This means that you can write scheme code that writes and modifies scheme code.

For example, take this function, which replaces the first element form a scheme expression with a +:

Note that we just treat the code like any other scheme list. To call this function, we can just run

Now, if we want to actually run this program, we can wrap it in an eval call as such:

Macros

You’ll note that in the above, we have to quote the arguments and then eval the result. It turns out that there’s a construct in Scheme that will do this for you! Using the same replacing with + function, we can define

Note that this is the same definition, except that we have replaced define with define-macro. Now, Scheme handles the quoting of the arguments and the evaluation of the result for us as such:

Pretty nifty, huh!

Infix notation

OK, but the post’s title is infix notation. Let’s say we want to be able to write (12 * (2 + 3)) in scheme and have it evaluate the way it would in Python. To accomplish this, let’s define a function (not a macro for now) that takes in (12 * (2 + 3)) and converts it into the scheme form (* 12 (+ 2 3)). First off, we need to identify which things are in fact infix notation:

The idea here is that we check that the given piece of code is a list with 3 elements, and that its middle element is an operator. Now, let’s write the code to convert infix to prefix notation.

Where this code just places the elements in second, first, third order.

Now, we can put it together with a recursive function:

The idea behind this code is that if something is infix, we should rearrange it, then call ourselves to finish up the task, if something is a call expression, we should just look at every element, and otherwise, we’re at a base case and can just return.

Let’s try this out on our example:

It works!

Finally, what we really want is a macro. We can just define one directly:

Sadly we can’t just (define-macro to-prefix to-prefix-func) because of a technicality in the scheme language. Anyway, now we can run our scheme code:

And there you have it. Scheme’s power might be in its simplicity but with great power comes the ability to create complexity. Obviously, the usual disclaimer applies: don’t write code like this, but if you do, do it with macros!

The code

A fully runnable version of this is below: try copy-pasting it into 61A’s scheme interpreter and check it out! (There are a few helpful functions defined at the end that we just kinda assumed the existence of above).

---

(Mini) Scheme in 50 Lines

18 Mar 2018

The scheme language is a programming language that is unique for being easy to parse. Every construct in scheme is of the form

Our Subset

We will start with some standard scheme expressions, which you can think about as being analogous to certain patterns in Python. For example instead of writing a + b, you write (+ a b), where + is just the name of a function. Similarly, instead of writing lambda x: x * 2 for the doubling function, you write (lambda (x) (* 2 x)). Just lambdas and function application are enough to perform any calculation, but we add a few more features for clarity: instead of x = y we write (define x y), instead of x if y else z we write (if y x z) and instead of writing

we write (begin (define x (f y)) x). The real scheme language has many more constructs, including ones that simulate python’s def statements, and some unique ones that allow you to assign variables in a local frame, simulate elif trees, have short-circuited and/or constructs, or even define your own language constructs. For brevity, we will stick to this subset, which is still very powerful.

Lexing

The first step in processing a scheme program is to split it up into a list of tokens. What we do is take an expression like '(a b (c))' and convert it into a list of tokens like '(', 'a', 'b', '(', 'c', ')', ')'.

To accomplish this, we first pad all the parentheses with space and replace all space-like characters with a space. We then split on spaces (and filter out empty tokens, which are produced when multiple spaces are consecutive).

Parsing

We now need to parse the string. If we have '(a b (c))', we want to parse it to ['a', 'b', ['c']] so we can process it in Python. Parsing scheme is fairly simple using recursion. Whenever we see a symbol or number, we just return and move on. Otherwise, we recursively call parse until we see an end parenthesis. For example, if we have the current state of our input

we parse by removing the ( from the front, then parse +, 2, (4), and (* 5 3) before seeing the unmatched ). Then we return, having removed everything but the 2 3). This is implemented as follows:

The reason we reverse the text is so that pop() pops from the end rather than the front of the input stream.

Frames

We need to define an environment diagram so that we can execute code. This is similar to a Python style environment diagram, which is a backwards pointing tree (children point towards the root via the parent annotation rather than the other way around).

To define a frame, we use the defaultdict class from python, which is like a dictionary except that when it can’t find a key, instead of raising a KeyError, it calls a 0 argument function you provide in the constructor and sets that as its value. We want to slightly modify this so that it calls a 1 argument function. Thus we define a frame as such:

defaultdict calls the __missing__ function when necessary, and in this case, it calls the parent function on a key. We can create a child frame for a given frame simply by saying frame(lambda v: parent[v]). We can now create a global frame as such:

We do something a little hacky here by basically defining integers as just being variables that evaluate to the integer version of themselves via the function int. (this works as int("123") == 123).

Special Forms

Now we need to somehow handle our special keywords (define, lambda, begin, if).

Define

We assume that we already have a function seval defined, which is the function that will eval a scheme expression. In scheme, define returns the variable being assigned to, for reasons of tradition.

Lambda

A lambda expression has no side effects, but must return a function. First we create a new frame, then we assign the operator to the operands, and then we run the body of the function in that frame and return the last value:

Begin

This is similar to lambda except that we don’t have any arguments or a new frame, and this one is simple enough to just write as a Python lambda function.

If

We can just directly map this to the equivalent Python construct.

Putting it together

We create a dictionary of special forms for easy access:

Eval Function

To evaluate a parsed scheme tree, what we need to do is dependent on whether the input is a list or not. If we have a list, then we need to check if its first element is a special form, and if so run its special form function. Otherwise, we evaluate the first item as a function, then evaluate the rest of the items as its arguments, then call the function. If we don’t have a list, we just look up the current element in the current frame.

We can then run scheme by running seval(parse(text)).

The Entire Interpreter

The entire interpreter, which is just 50 lines, is as below:

Of course, a proper scheme interpreter, which has more features (see the section “Subset”), more possible types (like strings, symbols, lists, etc.), and better error handling (we crash on a lot of cases with IndexErrors and ValueErrors). In fact, that’s an entire project in 61a.

But I personally enjoy that you can get quite a few features in such a small amount of space.

Try it out on the following program!

---

The Efficiency Gap Makes No Sense (but all metrics show Republicans are better at gerrymandering)

12 Jan 2018

Cracking, Packing, and Wasted Votes

The efficiency gap is a technique for measuring the level of gerrymandering in a state. Gerrymandering generally takes the form of what’s known as “cracking and packing.” Cracking is the process of taking a district with a majority of the opposing party and splitting it into two in which the party has a minority in each, thus denying your opponent that seat. However, this isn’t always possible because your opponent might have too many votes in a given area. To reduce the remaining number of votes your opponent has while minimizing the number of seats they have, you can use a technique called packing, in which you create a district in which your opponent can win by a huge margin.

To measure both cracking and packing, we can use the concept of a wasted vote. A wasted vote is any vote that did not contribute to the victory. There are two kinds of wasted votes, cracked waste and packed waste. A cracked wasted vote for party X is any vote in a district party X has lost. A packed wasted vote is any vote for party X over 50% in a district party X has won.

For example, let’s say that there are just two parties¹ and 1000 voters in a district. The number of wasted votes for X in terms of the number of votes for X is as such:

---

How You Get Homeopathy

05 Jan 2018

Homeopathy is a system that has two primary claims. The first is the law of similars. It says that a dilute solution of a substance cures the ailment caused by a concentrated solution of the same substance. The second is the law of dilution, which says that the more dilute a homeopathic preparation is, the stronger its effect.

The second theory is the one people tend to focus on because it is clearly incorrect. The anti-homeopathy \(10^{23}\) campaign is named after the order of magnitude of Avogadro’s number, that is the number of molecules of a substance in a 1M solution of a substance (typically a fairly strong solution, 1M saltwater is 5 teaspoons of salt in a liter of water). If you dilute by more than that amount, and many “strong” homeopathic preparations do, then with high probability you literally have 0 molecules of the active ingredient in your preparation. As the \(10^{23}\) campaign’s slogan makes clear, “There’s nothing in it” and homeopathic medicines are just sugar pills.

---

What is NP?

26 May 2017

What is P?

This seems like a silly question. This question seems easily answered by the surprisingly comprehensible explanation on P’s Wikipedia page:

It contains all decision problems that can be solved by a deterministic Turing machine using a polynomial amount of computation time

OK, so it’s the set of all decision problems (yes-or-no questions) that are \(O(n^k)\) for some integer \(k\). For example, sorting, which is \(\Theta(n \log n)\) is P, since it’s also \(O(n^2)\).

But let’s go for an alternate definition. Let’s take a C-like language and get rid of a bunch of features: subroutine calls, while loops, goto, for loops with anything other than i < n in the second field (where n is the length of the input), and modifying the for loop variable within the loop. Effectively, this language’s only loping construct is for(int varname = 0; varname < n; varname++) {/* Code that never modifies varname */}. Let’s call this language C-FOR.

---

Storing Data With the Circle-Tree

15 Jan 2017

The Pair Abstraction

Computers need some way to store information. More specifically, we want to be able to store multiple pieces of data in one place so that we can retrieve it later. For now, we’ll look at the simplest way of storing data, a pair.

To express the concept of a “pair”, we need three machines.

1. A way to put two things together (construction, or “C” for short)
2. A way to get the first element (first, or “F” for short)
3. A way to get the second element (second, or “S” for short)

---

Circle-Tree as a Calculator

13 Jan 2017

Using Circle-Tree Drawings as a Calculator

So this isn’t just a procrastination game for doodling when you’re bored (and have a lot of colored pencils, for some reason). We can use circle-tree as a way to express math!

Numbers

For math, the first thing we need are numbers. I’m just going to draw some pictures which are defined to be the numbers. We don’t worry too much about whether they are “really” numbers or not in the way that we don’t worry about whether “102” or “CII” is a better way to explain the concept of “how many cents in a dollar plus how many hands a person has”ness.¹

So this is 0:

---

Introducing the Circle-Tree System

21 Aug 2016

If you want to follow along on paper, you’ll want some colored pencils. Like at least 5 colors, not including a pencil to draw links.

Circtrees

In any case, we’ll call the diagrams we’re interested in “circtrees.”¹ Circtrees can be constructed in one of three ways.

1. Dots

A dot of any color is a circtree. Here are some examples²:

---

Counting Monoids

20 Jul 2016

What’s a Monoid?

A monoid is a set \(M\) with an identity element \(e : M\) and an operation \(* : M \to M \to M\), where we have the laws:

• \(x * e = x\)
• \(e * x = x\)
• \(x * (y * z) = (x * y) * z\)

We write a monoid as a tuple \((M, e, * )\). Some example monoids (written in pseudo-Haskell) are

---

The Porus Mirror Problem, Part 2

01 Jun 2016

Propagation

From last time, we know the quantity of light that escaped at each location and direction around the unit circle. We want to find how this translates into quantities of light at any point away from the circle. This situation can be modeled as so:

---

The Porus Mirror Problem, Part 1

29 May 2016

The porus mirror problem

I’m pretty sure I came up with this problem on my own, but I’m not sure if its an existing problem under a different name. Anyway, the situation is as such:

1. We have a very short cylindrical tube. In fact, we’ll ignore the third dimension and just use a circle. For simplicity, we’re using units such that the radius is 1.
2. The tube is filled with a gas that emits corpuscles in one large burst. We assume a large enough number that we can model them continuously. We additionally assume that the emmissions are uniform in location and direction.
3. The tube itself is semitransparent, with transparency determined by a function \(t: [0, 2\pi] \to [0, 1]\) of angle around the circle. Any light that does not pass through is reflected across the normal.

We wish to calculate at each point along the surface of the tube what is the total quantity of light emitted in each direction, from which we can easily calculate the light pattern this system will cast on any shape outside.

---

Dependent Types and Categories, Part 1

21 May 2016

So I’ve been trying to go through Category Theory for Scientists by writing the functions as code. So I obviously decided to use Haskell. Unfortunately, I ran into a wall: Haskell is actually pretty bad at representing categories.

Haskell is a Category

Now, at first this was incredibly surprising. Frankly, I had started learning about category theory because of its association with Haskell. Unfortunately, I didn’t realize that Haskell isn’t category theory, it’s a category.

For instance, look at this definition of a category in math:

---

Chaos, Distributions, and a Simple Function

19 May 2016

\(\newcommand{\powser}[1]{\left{ #1 \right}}\)

Iterated functions

The iteration of a function \(f^n\) is defined as:

\[f^0 = id\] \[f^n = f \circ f^{n-1}\]

For example, \((x \mapsto 2x)^n = x \mapsto 2^n x\).

Most functions aren’t all that interesting when iterated. \(x^2\) goes to \(0\), \(1\) or \(\infty\) depending on starting point, \(\sin\) goes to 0, \(\cos\) goes to something close to 0.739. \(\frac{1}{x}\) has no well defined iteration, as \((x \to x^{-1})^n = x \to x^{(-1)^n}\) which does not converge.

---

Haskell Classes for Limits

10 May 2016

OK, so the real reason I covered Products and Coproducts last time last time was to work toward a discussion of limits, which are a concept I have never fully understood in Category Theory.

Diagram

As before, we have to define a few preliminaries before we can define a limit. The first thing we can define is a diagram, or a functor from another category to the current one. In Haskell, we can’t escape the current category of Hask, so we instead define a diagram as a series of types and associated functions. For example, we can define a diagram from the category \(\mathbf 2\) containing two elements and no morphisms apart from the identities as a pair of undetermined types.

A diagram from the category \(\mathbf 2*\), a category containing two elements and an arrow in each direction (along with the identities), (this implies that the two arrows compose in both directions to the identitity):

---

Haskell Classes for Products and Coproducts

08 May 2016

Product Data Structures

Product Types are a familiar occurrence for a programmer. For example, in Java, the type int \(\times\) int can be represented as:

class IntPair {
    public final int first;
    public final int second;
    public IntPair(int first, int second) {
        this.first = first;
        this.second = second;
    }
}

---

Monoids, Bioids, and Beyond

07 May 2016

Two View of Monoids.

Monoids

Monoids are defined in Haskell as follows:

Monoids define some operation with identity (here called m_id). We can define the required laws, identity, and associativity, as follows:

---

Nontrivial Elements of Trivial Types

29 Apr 2016

We know that types can be used to encode how to make useful data structures.

For example, a vehicle can be encoded as:

In this case, valid values include cars with VINs and LPNs, or Bikes, which have neither of these data points.

However, some data types can seem far less useful.

---

The Autogeneration of Landscapes

23 Apr 2016

OK, so a break from theory and CS, and to applications. How do we produce reasonably realistic landscapes using differential equations?

Mountains and Valleys

To simulate mountains and valleys, we can use a fairly simple algorithm that adds a random amount to a region, then recursively calls itself on each quadrant of the region. Afterwards, an image generally looks something like:

We can apply a Gaussian blur to the image to get a reasonably realistic depiction of mountains and valleys.

We can define the elevation as a function \(E(x, y, t)\). Representing this as a landscape:

---

C-Style Pointer Syntax Considered Harmful

21 Apr 2016

Declaration Follows Use

In C, a pointer to int has type int*, but really, this isn’t the right way of looking at it. For example, the following declaration:

int* x, y;

creates x of type int* and y of type int.

---

The Triviality Norm

17 Apr 2016

Feynman famously said that to a mathematician, anything that was proven was trivial. This statement, while clearly a lighthearted dig at mathematics, it does have a striking ring of truth to it.

Logical Implication

In logic, there is the concept of implication. The idea is that if \(B\) is true whenever \(A\) is true we can say that \(A \implies B\). This makes sense for statements that depend on a variable. For example, we can say that \(x > 2 \implies x > 0\).

---

A Monadic Model for Set Theory, Part 2

16 Feb 2016

\(\newcommand{\fcd}{\leadsto}\)

Last time, we discussed funcads, which are a generalization of functions that can have multiple or no values for each element in their input.

Composition of Funcads

The composition of funcads is defined to be compatible with the composition of functions, and it takes a fairly similar form:

\[f :: Y \fcd Z \wedge f :: X \fcd Y \implies \exists (f \odot g :: X \fcd Z), (f \odot g)(x) = \bigcup_{\forall y \in g(x)} f(y)\]

In other words, map the second function over the result of the first and take the union. If you’re a Haskell programmer, you probably were expecting this from the title and the name “funcad”: the funcad composition rule is just Haskell’s >=>.

---

A Monadic Model for Set Theory, Part 1

16 Feb 2016

\(\newcommand{\fcd}{\leadsto}\)

Solving an Equation

A lot of elementary algebra involves solving equations. Generally, mathematicians seek solutions to equations of the form

\[f(x) = b\]

The solution that most mathematicians come up with to this problem is to define left and right inverses: The left inverse of a function \(f\) is a function \(g\) such that \(g \circ f = \mathrm {id}\). This inverse applies to any function that is one-to-one. There is also a right inverse, a function \(g\) such that \(f \circ g = \mathrm {id}\) For example, the left inverse of the function

\[x \mapsto \sqrt x :: \mathbb R^+ \rightarrow \mathbb R\]

is the function

\[x \mapsto x^2 :: \mathbb R \rightarrow \mathbb R^+\]

---

What is Category Theory?

28 Jan 2016

\(\newcommand{\mr}{\mathrm}\) So, I was reading Category Theory for Scientists recently and kept having people ask me: What is category theory? Well, until I hit chapter 3-4, I didn’t really have an answer. But now I do, and I realize that to just understand what it is doesn’t really require understanding how it works.

Sets and functions

So, set theory is all about sets and functions. Why are we talking about set theory and not category theory, you may ask? I’ll get to category theory eventually, but for now, let’s discuss something a little more concrete.

Let’s look at subsets of the set \(\{a, b\}\). We have the possibilities, which we name Empty, A set, B set, Universal set:

\[E = \{\}, A = \{a\}, B = \{b\}, U = \{a, b\}\]

---

Stupid Regex Tricks

31 Dec 2015

Regexes, the duct tape of CS

Regexes are truly amazing. If you haven’t heard of them, they are a quick way to find (and sometimes replace) some body of text with another body of text. The syntax, while it has its critics, is generally pretty intuitive; for example a zip code might be represented as

which is read as “a five digit code optionally followed by a spaced dash and a four digit code”. Some whitespace and named groups might help the reading (use COMMENTS mode when parsing)

---

Dictp Part 2

30 Dec 2015

OK, so to continue the Dictp saga, some syntactic sugar.

References to local variables.

The parser can be enhanced by rewriting anything that isn’t a built-in command or a string with a lookup to __local__.

E.g.,

• a \(\mapsto\) __local__['a']
• 0 = 1 \(\mapsto\) __local__['0'] = __local__['1']
• 0? \(\mapsto\) __local__['0']?
• '0' \(\mapsto\) '0'

---

Dictp Part 1

21 Dec 2015

So, a friend and I (I’m going to protect his anonymity in case he doesn’t want to be associated with the travesty that is what we ended up thinking up) were discussing ridiculous ideas for programming languages: you know the deal, writing C interpreters in Python, using only integers to represent everything, etc.

One idea, however, seemed a little less ridiculous to us (OK, just to me): a language in which there are two data types: Dictionary and String.

---

Infsabot Strategy Part 2

10 Dec 2015

OK, so to continue our Infsaboting.

Correction

I made a mistake last time. I included SwitchInt, a way to switch on values of ExprDir, which is ridiculous since an ExprDir can only be constructed as a constant or an if branch to begin with.

So just imagine that I never did that.

Guess and Check

OK, so how should our AI construct these syntax trees? At a very high level, we want to be able to 1) assess trees against collections of trees and 2) modify them randomly. We can represent this as a pair of types:

I think the implementation of asses should be pretty clear: simply find the win rate (given that we can simulate an unlimited number of games).

Modify, on the other hand, is a little more complicated. There are a few ways a tree can be modified:

• Modify the value of a constant to be something else.
• Modify the value of a field to point to something else or a field
• Add leaves to the tree
• Remove leaves as a simplification step

---

Infsabot Strategy Part 1

06 Dec 2015

OK, so what is this Infsabot? Infsabot is a game I designed for people to write programs to play. Basically, it’s like chess, except where each piece acts independently of each other.

The Game

There is a square board where each square is either empty or contains material. The game pieces, robots, require material to stay alive and perform tasks. At each turn, every robot reports which of the following it wants to do:

• Noop: The robot does nothing
• Die: The robot dies
• Dig: The robot digs to try to extract material
• Move: The robot can move in one of the four compass directions
• Fire: The robot can fire a quick-moving projectile (e.g., travel time = 0) in a compass direction
• Message: The robot can send a quick-moving message in a compass direction
• Spawn: The robot can create a new robot with its own initial material and appearance

To decide what to do, a robot has access to two things:

• A picture of the positions around it, to a given distance
  • Whether or not the spot contains material
  • Whether or not the spot contains a robot, and it’s appearance (not it’s team)
• A snapshot of its own hard drive, which is a massive relational database between Strings and Strings
• A list of all messages received

---

What's a number?

24 Nov 2015

OK, so a bit of a silly question. Of course, we all know what numbers are. But humor me, and try to define a number without using “number”, “quantity”, or anything that refers back to a number itself.

But, before we learn numbers, we have to first understand something simpler: counting. Couldn’t we define numbers in terms of counting? Well, yes, otherwise I wouldn’t be writing this article.

Now, to not end up with a forty page book, I’m only going to go over how to define the whole numbers (I’m going to ignore negative integers, fractions, \(\pi\), etc.)

---

Recursivized Types

23 Nov 2015

So, a short break from \(\varepsilon—\delta\).

Anyway, I’m going to look at Algebraic types in this section. Specifically, I am going to use Haskell types.

The provided code is all actual Haskell, in fact, I’m going to have to de-import the standard libraries because some of this is actually defined there. You can find all the code here

---

Who Needs Delta? Defining the Hyper-Real Numbers

19 Nov 2015

\(\renewcommand{\ep}{\varepsilon}\) \(\renewcommand{\d}{\mathrm d}\)

In high school Calculus, solving differential equations often involves something like the following:

\[\frac{\d y}{\d x} = \frac{y}{x}\]

\[\frac{\d y}{y} = \frac{\d x}{x}\]

\[\int \frac{\d y}{y} = \int \frac{\d x}{x}\]

\[\log y = c + \log x\]

\[y = kx\]

Now, I don’t know about anyone else, but this abuse of notation really bothered me at first. Everyone knows that \(\d x\) isn’t an actual number by itself, but we seem to use it all the time as an independent variable.

---

Ancient Greek Abstract Algebra: Introduction

06 Oct 2015

Note: I’ve put the Ancient Greek Abstract Algebra series on hold for now. Please take a look at some of my other post(s).

Modern constructions of \(\mathbb{N}\)

The natural numbers are taught to children as a basic facet of mathematics. One of the first things we learn is how to count. In fact, the name “Natural Numbers” itself implies that the natural numbers are basic.

However, modern mathematicians seem to have trouble with accepting the natural numbers as first class features of mathematics. In fact, there are not one but two common definitions of the naturals that can be used to prove the Peano Axioms (the basic axioms from which most of number theory can be proven).

---