Haskell Classes for Products and Coproducts

Product Data Structures

Product Types are a familiar occurrence for a programmer. For example, in Java, the type int \(\times\) int can be represented as:

class IntPair {
    public final int first;
    public final int second;
    public IntPair(int first, int second) {
        this.first = first;
        this.second = second;
    }
}

In C, the same type can be represented as:

typedef struct {
    const int first, second;
} int_pair;

In Haskell, it can be represented as

data IntPair = IntPair Int Int

Of course, a general product data type can also be defined in many languages. For brevity I am only going to include the Haskell version:

data P a b = P a b

P is therefore a generic way to construct a product of any two types.

Products in Category Theory

The above definitions of a product require a notion of elements of our objects (in this case types), which doesn’t make much sense for categories in general.

Spans

But we can define a span as two morphisms from the generic container to the two values. As a picture:

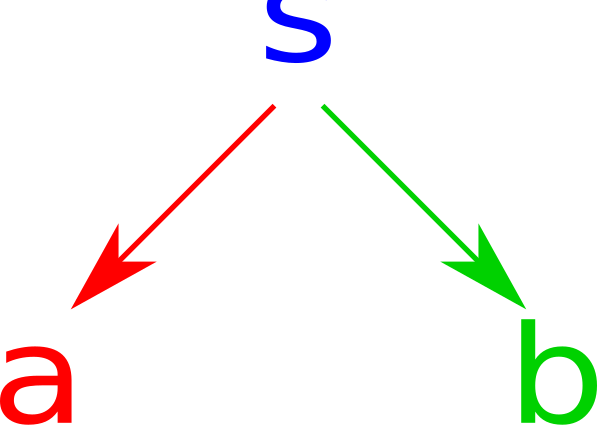
In Haskell, we want to make sure that our s has some connection to a and b so we parametrize it as so:

class Span s where
    fst :: s a b -> a
    snd :: s a b -> b

We can recover the traditional definitions of fst and snd as follows:

instance (Span (,)) where
    fst (x, _) = x
    snd (_, y) = y

In any case, a span is not sufficient to determine a product. We can also define instances for the following:

instance (Span ((,,) a)) where
    fst (_, x, _) = x
    snd (_, _, y) = y

Obviously, this is not a valid product, as it is inhabited by values with three distinct types.

A Categorical Product

In category theory, a product is defined as \(c\) in the following diagram (where a dashed line implies only one possible morphism).

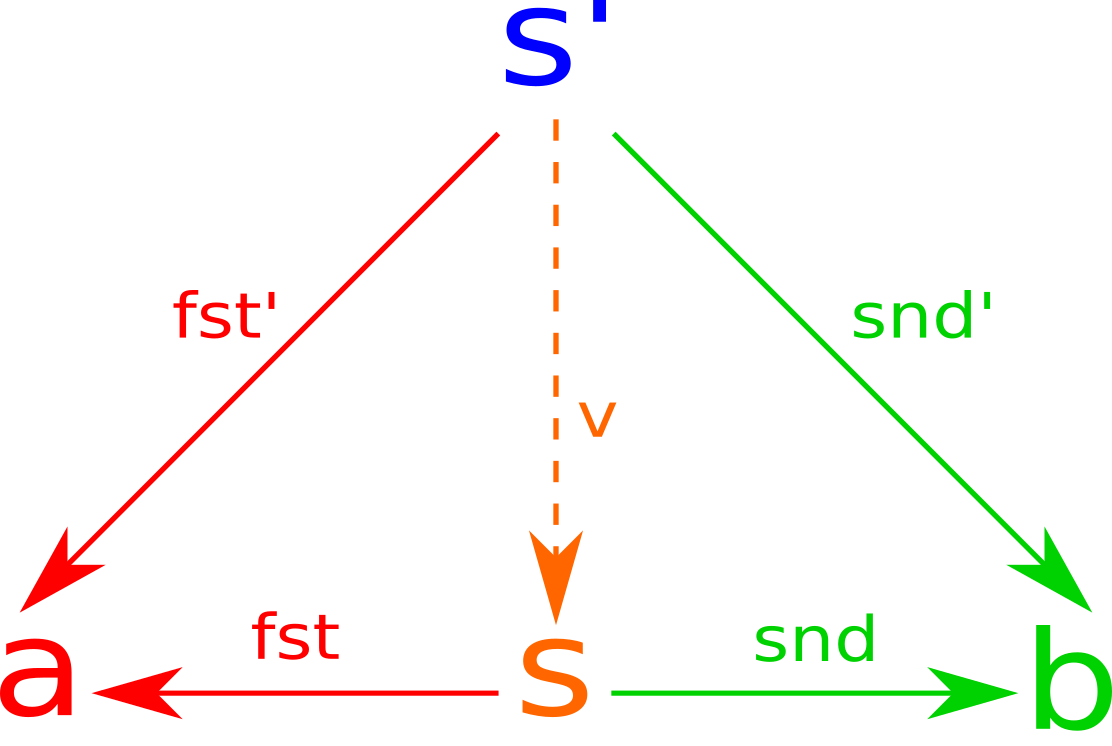
In any case, we have to define some function \(v\) for any span \(s’\) such that

\[\text{fst} \circ v = \text{fst}’\] \[\text{snd} \circ v = \text{snd}’\]

In any case, we have the following Haskell definition, with the given law as well as the implicit law that there be only one way to implement pFactor.

class (Span s) => Product s where
    pFactor :: (Span s') => s' a b -> s a b

lawProduct :: forall s s' a b. (Eq a, Eq b, Span s', Product s) => s' a b -> Bool
lawProduct val' = fst val == fst val' && snd val == snd val'
    where
    val :: s a b
    val = pFactor val'

We can confirm that tuples are indeed products.

instance Product (,) where
    pFactor val' = (fst val', snd val')

Note that there is no way to make (_, x, y) a product, because one would need to put a value into the first box of type forall a. a and there is no value of that type apart from undefined. If we use the type (Int, x, y) instead, we have several potential implementations, one for each value of Int. If we however use ((), x, y) we have a valid product:

instance Product ((,,) ()) where
    pFactor val' = ((), fst val', snd val')

This type is completely isomorphic to (x, y), so it is too a product. Since the () type has one element, this isomorphism is equivalent to 1 * x * y = x * y.

Coproducts

A common thing to do in category theory is to reverse all the arrows and see what happens. Doing so for a span gives us a cospan, which looks like this:

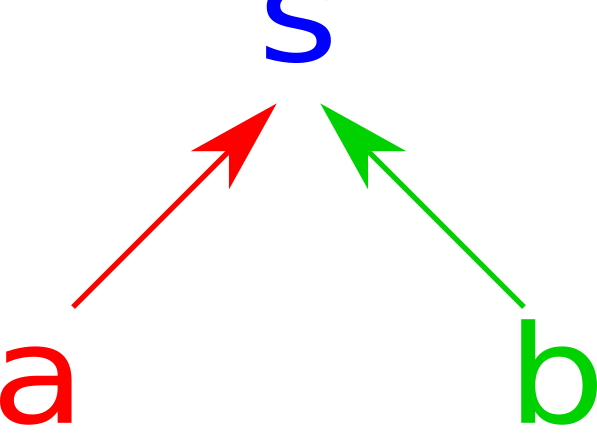
and can be implemented like this:

class Cospan s where
    left :: a -> s a b
    right :: b -> s a b

Each of the functions defines a constructor. We can make Either an instance of Cospan by delegating left and right to constructors.

instance Cospan Either where
    left = Left
    right = Right

We can also define a triple choice function that is a cospan:

data TripleEither a b c = A a | B b | C c
    deriving (Show, Eq)

instance Cospan (TripleEither a) where
    left = B
    right = C

We can define a coproduct in a similar manner: by inverting the arrows of a product diagram.

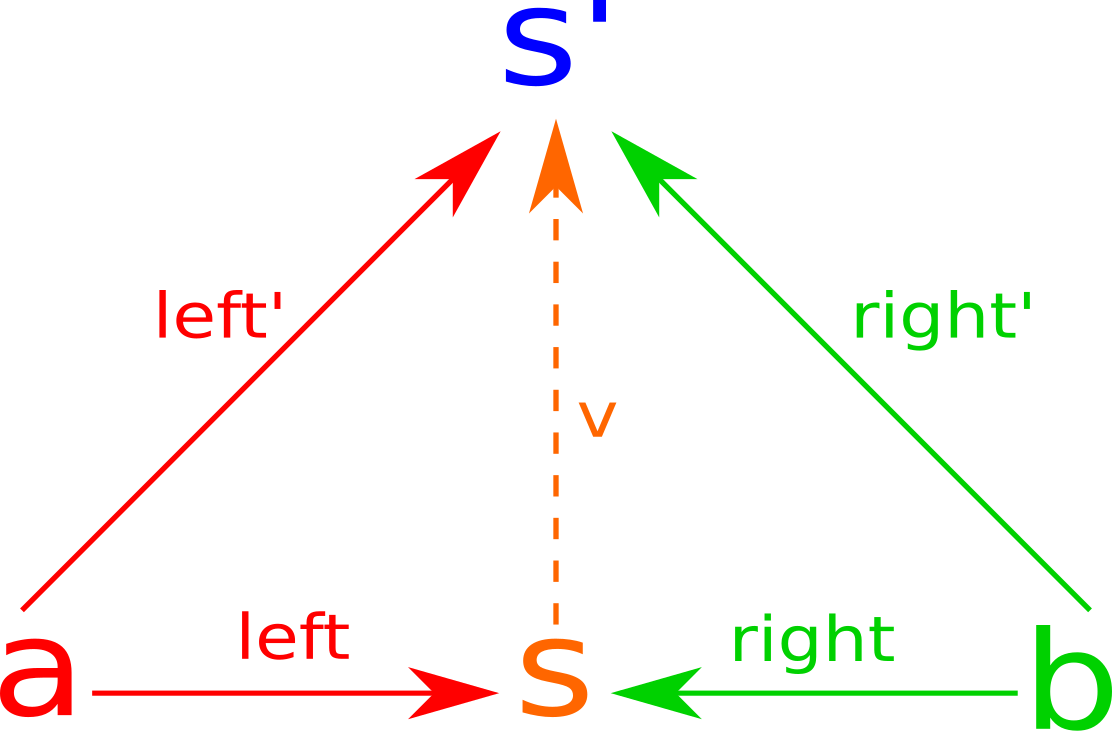
In any case, we must have a function from the coproduct to any span

class (Cospan s) => Coproduct s where
    cpFactor :: (Cospan s') => s a b -> s' a b

lawCoproduct :: forall s s' a b. (Eq (s' a b), Cospan s', Coproduct s) => a -> b -> Bool
lawCoproduct a b = cpFactor lhsA == rhsA && cpFactor lhsB == rhsB
    where
    rhsA, rhsB :: s' a b
    rhsA = left a
    rhsB = right b
    lhsA, lhsB :: s a b
    lhsA = left a
    lhsB = right b

We can therefore implement Either as a coproduct as follows:

instance Coproduct Either where
    cpFactor (Left a) = left a
    cpFactor (Right a) = right a

Unlike before, there is no possible implementation for TripleEither U for any concrete type U. We would need to coerce a value of type U to a random value. However, we can take a hint from our Product Isomorphism and use the type with 0 elements, or Void as follows:

instance Coproduct (TripleEither Void) where
    cpFactor (A v) = absurd v
    cpFactor (B b) = left b
    cpFactor (C c) = right c

This implementation makes use of absurd, a function that takes advantage of the impossibility of generating a Void to basically bypass that scenario entirely.

Conclusion

And there we have it, a categorical product and coproduct system defined in Haskell. If you want to try these out, you can find the source code here.