A Monadic Model for Set Theory, Part 2

\(\newcommand{\fcd}{\leadsto}\)

Last time, we discussed funcads, which are a generalization of functions that can have multiple or no values for each element in their input.

Composition of Funcads

The composition of funcads is defined to be compatible with the composition of functions, and it takes a fairly similar form:

\[f :: Y \fcd Z \wedge f :: X \fcd Y \implies \exists (f \odot g :: X \fcd Z), (f \odot g)(x) = \bigcup_{\forall y \in g(x)} f(y)\]

In other words, map the second function over the result of the first and take the union. If you’re a Haskell programmer, you probably were expecting this from the title and the name “funcad”: the funcad composition rule is just Haskell’s >=>.

Anyway, here are a few examples of funcad compositions (originals in blue, red. output in green.):

Two functional, total funcads

These compose like regular functions

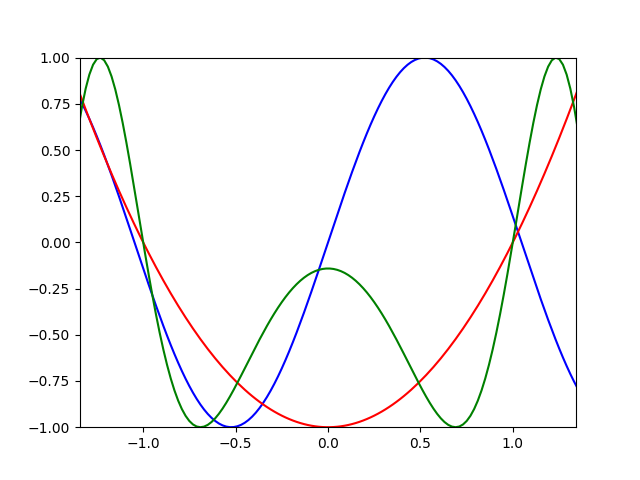
Composing a funcad with its inverse

We can represent the operator:

\[\star :: (A \fcd B) \to (A \fcd A)\] \[\star f = f^{-1} \odot f\]

Examples

\[f(x) = {x^2}\]

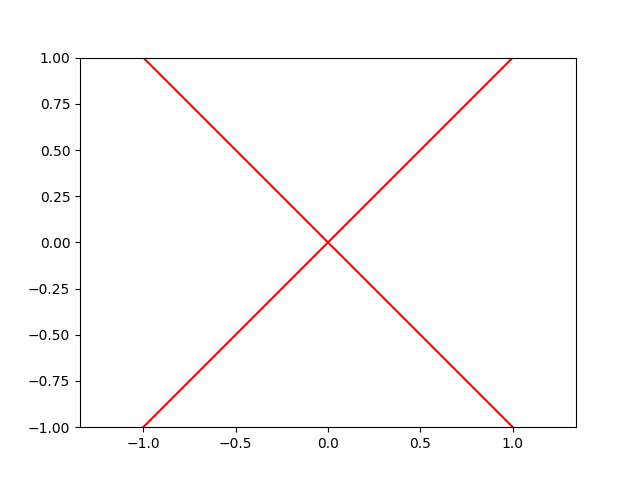
\[f(x) = \sqrt x\]

\[f(x) = \{y | x-1 \leq y \leq x + 1 \}\] \[f^{-1}(x) = \{y | x \in f(y)\} = \{y | y - 1 \leq x \leq y + 1 \}\] \[\star f (x) = \{y | y - 1 \leq z \leq y + 1, z \in \{t | x - 1 \leq t \leq x + 1\}\} \] \[\star f (x) = \{y | y - 1 \leq z \wedge z \leq y + 1, x - 1 \leq z \leq x + 1\} \] \[\star f (x) = \{y | y \leq z + 1 \wedge z - 1 \leq y, x - 1 \leq z \leq x + 1\} \] \[\star f (x) = \{y | y \leq x + 2 \wedge x - 2 \leq y\} \] \[\star f (x) = \{y | x - 2 \leq y \leq x + 2\} \]

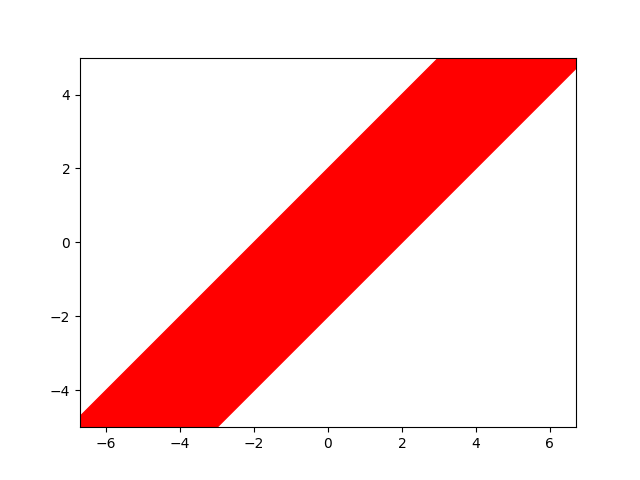
General Characterization

In general, \(\star\) represents the well-behavedness of the given funcad under under iversion.

We can find that

\[\star f(x) = f^{-1} \odot f (x) = \bigcup_{\forall y \in f(x)} f^{-1}(y)\] \[\star f (x) = \bigcup_{\forall y \in f(x)} f^{-1}(y)\]

Basically, \(\star f\) represents how one-to-one \(f\) is.

For any isomorphism \(f\), we have \(\star f(x) = x\).

For any one-to-one and functional funcad, we have

\[\star f(x) = \bigcup_{\forall y \in f(x)} f^{-1}(y) = \bigcup_{\forall y \in f(x), |f(x)| = 1, |f^{-1}(y)| = 1} f^{-1}(y)=\left\{\begin{array}{cc} \{x\} & \text{if \(|f(x)| = 1\)}\\ \{\} & \text{otherwise} \end{array}\right.\]

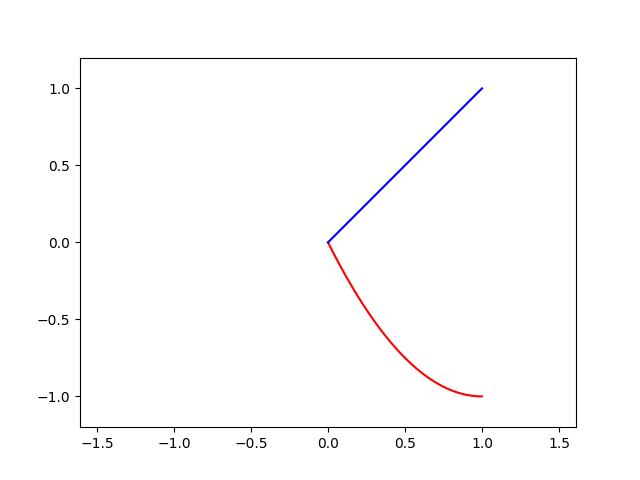
For example, for \(f(t) = \{t^2 - 2t\}, 0 \leq t \leq 1\), \(\star f(t) = t, 0 \leq t \leq 1\):

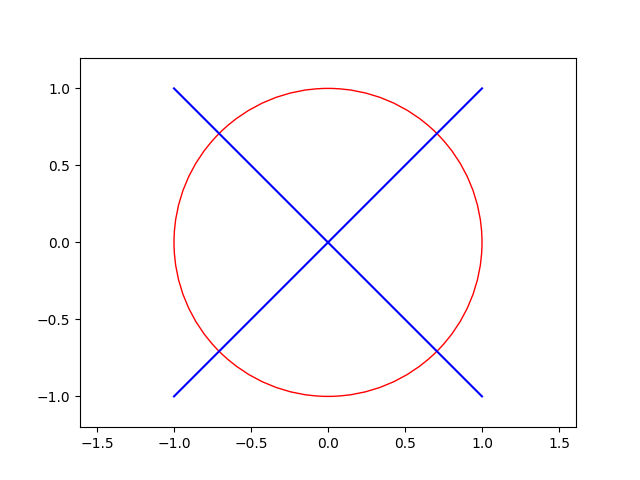
For a more complex funcad, such as \(f(x) = \pm \sqrt{1-x^2}\), we have \[\star f(x) = f^{-1}(\sqrt{1 - x^2}) \cup f^{-1}(-\sqrt{1-x^2}) = \pm x, -1 \leq x \leq 1\]

A Quick Coding Sample

So, we now know a few things about funcads. How about we put this knowledge into effect?

So, Funcads are Monads, and the typical set-like monad used in Haskell is a list where we don’t care about order or duplication. Therefore, we can define:

import Prelude hiding ((.))
import Control.Category

data Funcad a b = Funcad (a -> [b])
instance Category Funcad where
    id = Funcad return
    Funcad a . Funcad b = Funcad $ \x -> b x >>= a