The Autogeneration of Landscapes

OK, so a break from theory and CS, and to applications. How do we produce reasonably realistic landscapes using differential equations?

Mountains and Valleys

To simulate mountains and valleys, we can use a fairly simple algorithm that adds a random amount to a region, then recursively calls itself on each quadrant of the region. Afterwards, an image generally looks something like:

We can apply a Gaussian blur to the image to get a reasonably realistic depiction of mountains and valleys.

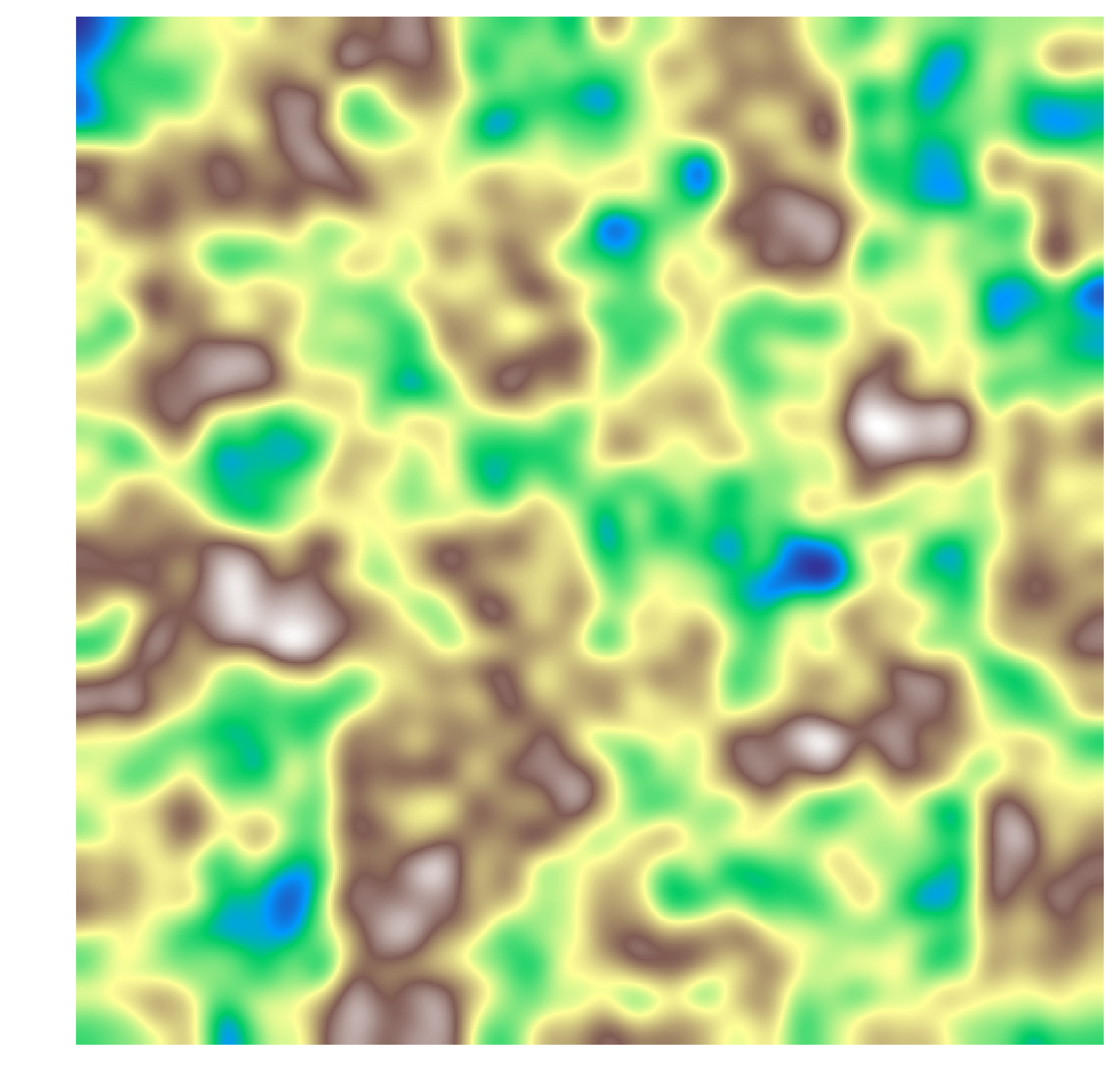
We can define the elevation as a function \(E(x, y, t)\). Representing this as a landscape:

Water

We can define the water level as a function \(W(x, y, t)\) representing the depth of water above land at that point.

We will assume for now that the amount of water is much smaller than the level of land. Therefore, we can represent the water flow over a single pixel as:

\[v(x, y, t) = k_1 \nabla E (x, y, t)\]

And we can define the water level as:

\[W(x, y, t + 1) = [W(x+1, y, t) - W(x-1, y, t), W(x, y+1, t) - W(x, y-1, t)] \cdot v(x, y, t)\]

Or more compactly,

\[\Delta_t W = k_1 [\Delta_x W, \Delta_y W] \cdot \nabla E\]

Adding in rain (a function \(R(x, y, t)\)), we get:

\[\Delta_t W = k_1 \nabla W \cdot \nabla E + R\]

And we can define, using erosion,

\[\Delta_t E = k_2\|v\| W \]

Erosion

A few changes had to be made to make the model workable. For example, the water had to stop flowing at minima. And then I had to edit the configuration.

The erosion model worked out pretty well, I think. Here’s a picture of the final result:

(This ended up being a bigger project than I had suspected. See the repo for the full source code).